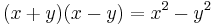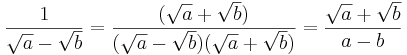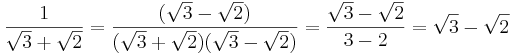Konjugat (algebra)

Från Rilpedia

(Omdirigerad från Konjugat (Algebra))
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

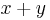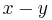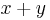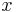Inom algebra bildas konjugatet till ett binom x + y\ genom att tecknet växlas för en av termerna, till exempel är x - y\ konjugatet till x + y\ . Om \ x är reellt och 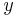\ y rent imaginärt bildas ett komplexkonjugat och där teckenväxlingen sker för den imaginära termen.

Konjugatregeln

Produkten av ett binom med dess konjugat blir enligt konjugatregeln differensen mellan två kvadrater

(x + y)(x - y) = x^2 - y^2 \

Rationalisering av nämnare

Rationalisering av nämnaren i ett bråk innebär att man gör en irrationell nämnare rationell, och i sin tur blir täljaren (oftast) irrationell. Detta lyckas ibland genom förlängning med täljarens konjugat. Exempel:

\frac{1}{\sqrt{a} - \sqrt{b}} = \frac{(\sqrt{a} + \sqrt{b})}{(\sqrt{a} - \sqrt{b})(\sqrt{a} + \sqrt{b})} = \frac{\sqrt{a} + \sqrt{b}}{a-b}


\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{(\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2})(\sqrt{3} - \sqrt{2})} = \frac{\sqrt{3} - \sqrt{2}}{3-2} = \sqrt{3} - \sqrt{2}


Nuvola apps edu mathematics-p.svg Denna artikel om algebra är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Konjugat_(algebra)"
Personliga verktyg
På andra språk