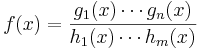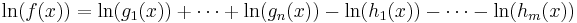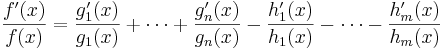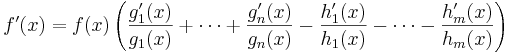Logaritmisk derivering

Från Rilpedia

Texten från svenska Wikipedia

Vid derivering av vissa funktioner kan logaritmisk derivering vara en räkneteknik som kan reducera räknearbetet markant. Speciellt väl fungerar den om uttrycket består av ett antal väl avgränsade enheter som multiplicerats ihop.

Exempel:

$f(x)=\frac{g_1(x)\cdots g_n(x)}{h_1(x) \cdots h_m(x)}$

Tag logaritmen:

$\ln(f(x))=\ln(g_1(x))+ \cdots +\ln(g_n(x))-\ln(h_1(x))- \cdots - \ln(h_m(x))$

Derivera:

$\frac{f'(x)}{f(x)}= \frac{g'_1(x)}{g_1(x)} + \cdots + \frac{g'_n(x)}{g_n(x)} - \frac{h'_1(x)}{h_1(x)} - \cdots - \frac{h'_m(x)}{h_m(x)}$

Härur löses $f'(x)$ enkelt och ger.

$f'(x)= f(x) \left ( \frac{g'_1(x)}{g_1(x)} + \cdots + \frac{g'_n(x)}{g_n(x)} - \frac{h'_1(x)}{h_1(x)} - \cdots - \frac{h'_m(x)}{h_m(x)} \right )$

I allmänhet ser naturligtvis uttrycken inte så trevliga ut som exemplet, men det kan ändå vara en hjälp för att derivera deluttryck.

Logaritmisk derivering

Från Rilpedia

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk