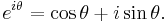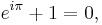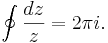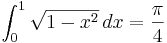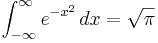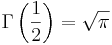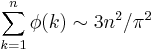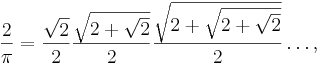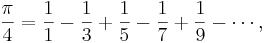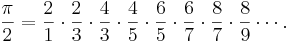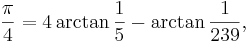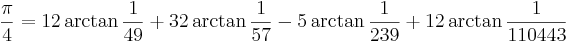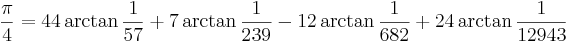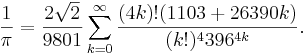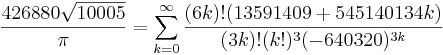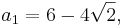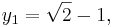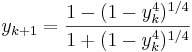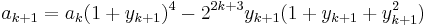Pi

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Den gemena bokstaven pi som används som symbol för detta tal.

Artikeln här handlar om talet pi; för annat se Pi (olika betydelser).

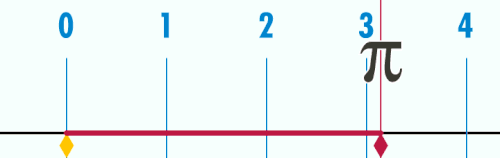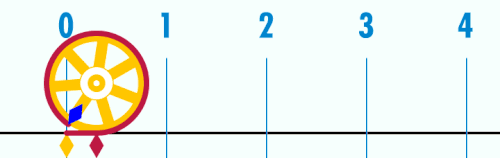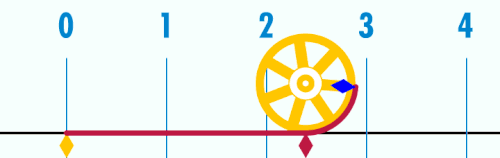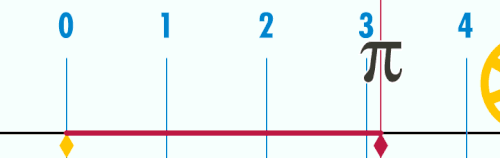
Talet π (eller pi i typografiska sammanhang där den grekiska bokstaven inte finns tillgänglig) är en matematisk konstant som bland annat representerar förhållandet mellan en cirkels omkrets och diameter. Dess värde är med 10 decimalers noggrannhet 3,1415926536 och avrundas ofta till 3,14, även om decimalerna fortsätter i oändligheten utan att uppvisa någon regelbundenhet. Talet är irrationellt (det kan inte skrivas som ett bråk), och dessutom transcendent (det kan inte uttryckas algebraiskt) vilket bland annat leder till att cirkelns kvadratur är ett problem som inte går att lösa. Utöver dessa egenskaper är π intressant eftersom det dyker upp på många olika håll inom matematiken, somliga till synes helt utan koppling till det geometriska ursprunget. Talet har studerats av framstående matematiker under alla tider, men flera frågor är ännu ouppklarade.

Den oändliga decimalutvecklingen har i sig fascinerat länge. Trots att de första 50 decimalerna räcker för att beräkna det synliga universums omkrets med en noggrannhet av en atomkärnas storlek har det blivit något av en tävling i att beräkna π med så många decimaler som möjligt – det senaste rekordet ligger på 1 241 100 000 000 stycken och sattes av den japanske matematikern Yasumasa Kanada år 2002 med hjälp av en superdator.^[1] Talet kallas även Arkimedes konstant efter Arkimedes, som 250 f.Kr. fann att dess värde låg inom det jämförelsevis snäva intervallet mellan 223/71 och 22/7, och Ludolphs tal efter Ludolph van Ceulen som kring år 1600 räknade ut 35 decimaler. In på 1900-talet var det inte ovanligt att använda approximationen 22/7 (ungefär 3,143) i beräkningar, vilket kan härledas till Arkimedes.

Beteckningen π, som härstammar från det grekiska ordet περιφέρεια (periferi), valdes 1706 av William Jones för att beteckna talet och standardiserades samma århundrade genom Leonhard Euler. Det råder delade meningar över huruvida tecknet π ska skrivas i kursiv eller rak stil (SIS rekommenderar rak stil).

Innehåll

1 Matematiska egenskaper
2 Formler där π uppträder
3 Kedjebråk
4 Historik
5 Formler för datorberäkningar
6 Mindre exakta uppskattningar
7 π-kultur
- 7.1 Populärkultur
- 7.2 Anhängare
8 Se även
9 Referenser

Matematiska egenskaper

Att π är irrationellt bevisades 1761 av Johann Heinrich Lambert. Dess transcendens bevisades 1882 av Ferdinand von Lindemann.

Den mest gäckande ouppklarade frågan är huruvida π är normalt, det vill säga om alla siffror och sifferkombinationer, i alla baser, förekommer med samma sannolikhet som om talet vore helt "slumpmässigt". Statistiska undersökningar av miljardtals siffror som beräknats med datorer pekar åt det hållet, men matematiska bevis saknas. David H. Bailey och Richard E. Crandall visade dock 2000 att π är normalt i basen två om en trolig hypotes från kaosteorin är sann. [1]

Det är också okänt huruvida π och e är algebraiskt oberoende, men det är känt att åtminstone det ena av πe och π + e är transcendent. Talet e^π, kallat Gelfonds konstant, är dock transcendent.

Formler där π uppträder

Geometri

π förekommer i många geometriska formler för cirklar, sfärer och andra runda objekt.

	Geometrisk form	Formel
	Omkretsen av en cirkel med radien r och diametern d	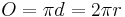$O = \pi d = 2 \pi r \,\!$
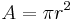	Arean av en cirkel med radien r	$A = \pi r^2 \,\!$
	Arean av en ellips med halvaxlarna a och b	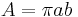$A = \pi a b \,\!$
	Volymen av en sfär med radien r och diametern d	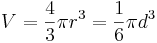$V = \frac{4}{3} \pi r^3 = \frac{1}{6} \pi d^3 \,\!$
	Ytarean av en sfär med radien r	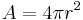$A = 4 \pi r^2 \,\!$
	Volymen av en cylinder med höjden h och radien r	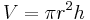$V = \pi r^2 h \,\!$
	Ytarean av en cylinder med höjden h och radien r	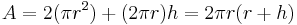$A = 2 ( \pi r^2 ) + ( 2 \pi r ) h = 2 \pi r (r + h) \,\!$
	Volymen av en kon med höjden h och radien r	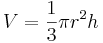$V = \frac{1}{3} \pi r^2 h \,\!$
	Ytarean av en kon med höjden h och radien r	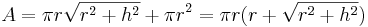$A = \pi r \sqrt{r^2 + h^2} + \pi r^2 = \pi r (r + \sqrt{r^2 + h^2}) \,\!$

180° (grader) motsvarar π radianer.

Analys

Talet π är intimt förbundet med de komplexa talen, vilket följer av de trigonometriska funktionernas förekomst i Eulers formel för den komplexa exponentialfunktionen,

$e^{i \theta} = \cos \theta + i \sin \theta.\,$

Ett specialfall är Eulers identitet,

$e^{i \pi} + 1 = 0,\,$

som kallades "den märkligaste formeln inom matematiken" av Richard Feynman för att den knyter samman fem av de viktigaste talen: 0, 1, e som är basen för den naturliga logaritmen, den imaginära enheten i utifrån vilken de komplexa talen definieras, och π. Vidare följer exempelvis av residualteoremet för kurvintegraler att

$\oint\frac{dz}{z}=2\pi i.$

Arean av en kvarts enhetscirkel ges av:

$\int_0^1 \sqrt{1-x^2}\,dx = {\pi \over 4}$

Övrig matematik

En integralformel, (se normalfördelning):

$\int_{-\infty}^{\infty} e^{-x^2}\,dx = \sqrt{\pi}$

Baselproblemet, först löst av Euler (se även Riemanns zeta-funktion):

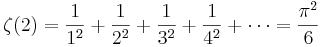
$\zeta(2) = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{\pi^2}{6}$

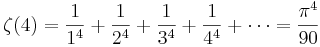
$\zeta(4)= \frac{1}{1^4} + \frac{1}{2^4} + \frac{1}{3^4} + \frac{1}{4^4} + \cdots = \frac{\pi^4}{90}$

Generellt är

ζ(2 n)

en rationell multipel av

π 2 n

för det positiva heltalet n

Gammafunktion utvärderad vid 1/2:

$\Gamma\left({1 \over 2}\right)=\sqrt{\pi}$

Stirlings formel:

$n! \sim \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n$

Egenskapen av Eulers phi-funktion (se även Fareysekvens):

$\sum_{k=1}^{n} \phi (k) \sim 3 n^2 / \pi^2$

Fysik

Kedjebråk

Den enkla kedjebråksframställningen av π börjar [3, 7, 15, 1, 292, 1, 1, 2, 1, 3, 1, 14, 1, 1, 2, 2, 2, 2, ...], och uppvisar ingen regelbundenhet. Genom trunkering av kedjebråket fås de rationella approximationerna 3, 22/7, 333/106, 355/113, 103993/33102, ... för π, som i respektive ordning ger 0, 2, 4, 6, 9, ... korrekta decimaler.

Historik

Arkimedes metod för att uppskatta π. Genom att stänga in en cirkel mellan två regelbundna polygoner fås en undre och en övre gräns för omkretsen eller arean och därmed även för π. I illustrationen visas sådana uppskattningar utförda med 5-, 6-, respektive 8-hörningar, vilka ger successivt bättre värden. Arkimedes använde sig av en konstruktion motsvarande en 96-hörning.

De tidigaste kända uppskattningarna av π:s värde härstammar från tiden cirka två årtusenden f.Kr. då babylonierna använde värdet 25/8 = 3,125, och egyptierna enligt Rhindpapyrusen uppskattade π till 256/81 ≈ 3,16. Arkimedes överträffade cirka 250 f.Kr. dessa resultat då han med en geometrisk konstruktion visade att π måste ligga mellan 223/71 och 22/7, motsvarande en noggrannhet på tre decimaler. Betydande framsteg gjordes under nästföljande dryga 1500 år av islamska, kinesiska och indiska matematiker, kulminerande cirka 1400 med Madhavas beräkning av 11 korrekta decimaler, överträffad av Ghiyath al-Kashis 16 några år senare.

Den matematiska analysen gav upphov till serier och iterationer för π:s exakta värde som i princip gör det möjligt att beräkna talet med önskad precision. Exempel är François Viètes formel från 1593

$\frac2\pi= \frac{\sqrt2}2 \frac{\sqrt{2+\sqrt2}}2 \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2\ldots,$

Gottfried Leibniz' formel

$\frac{\pi}{4} = \frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots,$

och John Wallis' produkt

$\frac{\pi}{2} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots.$

Den tyske 1500-talsmatematikern Ludolph van Ceulen vigde större delen av sitt liv åt att beräkna π med Arkimedes metod, och lyckades bestämma 35 decimaler. Först att nå 100 decimaler var John Machin, som 1706 använde den nu berömda Machins formel,

$\frac{\pi}{4} = 4 \arctan\frac{1}{5} - \arctan\frac{1}{239},$

kombinerad med Taylorserien för arctan. Efter honom lyckades 1800-talets matematiker beräkna hundratals decimaler för hand. Sedan mitten av 1900-talet har datorer gjort det möjligt att beräkna tusentals, miljontals, miljardtals och biljoner decimaler av π.

Formler för datorberäkningar

De mest effektiva formlerna för att med datorers hjälp beräkna π är i dag följande:

Machin-liknande formler

Machins formel är i datorernas era fortfarande praktisk för att beräkna π. Dock finns en hel familj av Machin-liknande formler för π, bestående av liknande summor av arctan-funktionen, varav somliga är mer effektiva än Machins ursprungliga. För det nuvarande rekordet på över 1 biljon decimaler (1 241 100 000 000) av π, satt 2002 av Yasumasa Kanada med kollegor vid Tokyos universitet, användes följande Machin-liknande formler med fyra termer:

$\frac{\pi}{4} = 12 \arctan\frac{1}{49} + 32 \arctan\frac{1}{57} - 5 \arctan\frac{1}{239} + 12 \arctan\frac{1}{110443}$

och

$\frac{\pi}{4} = 44 \arctan\frac{1}{57} + 7 \arctan\frac{1}{239} - 12 \arctan\frac{1}{682} + 24 \arctan\frac{1}{12943}$

Den ena formeln användes till en första uträkning, den andra för att kontrollera resultatet. Beräkningarna gjordes av en 64-noders superdator från Hitachi med 1 terabyte minne och kapaciteten att utföra 2 · 10¹² operationer per sekund. Beräkningarna tog 602 timmar. En normal utskrift av alla decimalerna skulle fylla 300 miljoner A4-papper.^[2]

Ramanujans och Chudnovskys serier

Srinivasa Ramanujan upptäckte en mängd oändliga serier för π, exempelvis den snabbt konvergerande

$\frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum^\infty_{k=0} \frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}.$

Baserat på Ramanujans resultat upptäckte bröderna Chudnovsky formeln

$\frac{426880 \sqrt{10005}}{\pi} = \sum^\infty_{k=0} \frac{(6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 (-640320)^{3k}}$

som de använde för att slå flera beräkningsrekord i slutet av 1980-talet, inklusive att 1989 komma först över en miljard decimaler av π. Chudnovskys formel används idag exempelvis av programmen Mathematica och Pifast för att beräkna π.

Iterationer

Två iterationer för att beräkna π är Brent–Salamins algoritm och Borweins algoritm. Borweins algoritm går exempelvis ut på att sätta (Brent–Salamins algoritm har en liknande form)

$a_1 = 6 - 4\sqrt{2},$

$y_1 = \sqrt{2} - 1,$

och sedan iterera

$y_{k+1} = \frac{1-(1-y_k^4)^{1/4}}{1+(1-y_k^4)^{1/4}}$

$a_{k+1} = a_k(1+y_{k+1})^4 - 2^{2k+3} y_{k+1} (1 + y_{k+1} + y_{k+1}^2)$

tills önskad noggrannhet uppnåtts och uppskattningen av π därefter ges av 1/a_n. Fördelen med dessa iterationer gentemot ovan nämnda summationer är att deras konvergens är superlinjär (Se exponentiell): antalet korrekta siffror som läggs till vid varje steg inte är konstant utan ökar. Brent–Salamins algoritm har kvadratisk konvergens, vilket innebär att antalet korrekta siffror fördubblas varje steg – Borweins algoritm till och med fyrdubblar antalet siffror. Nackdelen är att rötterna som ingår är tidskrävande att beräkna. Brent–Salamins och Borweins algoritmer användes 1999 för att beräkna respektive kontrollera 206 158 430 000 decimaler av π, vilket då var ett nytt rekord.

Direkt bestämning av siffror

David H. Bailey, Peter Borwein och Simon Plouffe hittade år 1995 en formel som gör det möjligt att direkt beräkna en godtycklig siffra i π:s binära representation utan att först behöva beräkna de föregående. De binära siffrorna kan översättas till motsvarande i baserna 4, 8, 16 och så vidare (dock ej till 10 för att få fram decimalerna):

$\pi = \sum_{k = 0}^{\infty} \frac{1}{16^k} \left( \frac{4}{8k + 1} - \frac{2}{8k + 4} - \frac{1}{8k + 5} - \frac{1}{8k + 6}\right)$

Formeln är känd som BBP-formeln, och flera liknande formler har härletts för π såväl som för andra konstanter. En mer effektiv version, Bellards formel, användes av det distribuerade projektet Pihex för att år 2000 beräkna 64 binära siffror i följd omkring den tusenbiljonte (som råkar vara 0).

Simon Plouffe upptäckte 1997 även en algoritm för att beräkna den n:te decimalen av π direkt, men den är dessvärre så långsam att den bara är praktisk för n upp till några tusen. En förbättring av Fabrice Bellard gör metoden praktisk för n upp till några miljoner, och Xavier Gourdon har hittat en metod som är ytterligare något snabbare. Trots dessa framsteg är det snabbaste sättet att bestämma den n:te decimalen fortfarande att beräkna π med alla föregående siffror och plocka ut den sista. [2]

Mindre exakta uppskattningar

En referens till π finns i Gamla testamentet i Bibeln:

Han gjorde vidare Havet i gjutgods. Det var cirkelrunt och mätte tio alnar från kant till kant; det var fem alnar högt och 30 alnar i omkrets. 1 Kung 7:23 N

Många skeptiker anser att enligt detta påstående skall π vara exakt 3, vilket de poängterat då de kritiserat Bibelns riktighet. Ekvationen diameter=10, omkrets=30 tillfredsställs dock av alla värden på diameter mellan 9,5 och 9,708 vid avrundning till närmaste heltal. En annan förklaring som cirka år 150 framfördes av den hebreiska rabbin och matematikern Nehemiah är att diametermåttet skulle kunna avse avståndet mellan ytterkanterna medan omkretsen mättes längs innerkanten.

En läkare och amatörmatematiker vid namn Edward J. Goodwin från delstaten Indiana i USA trodde att π:s transcendenta värde var felaktigt, och lade 1897 fram ett förslag på att bland annat lagstifta följande "nya matematiska sanningar":

Förhållandet mellan en cirkels diameter och omkrets är 5/4 till 4. (π = 3,2)

Förhållandet mellan längden på en 90 graders cirkelbåge och avståndet mellan dess ändpunkter är 8 till 7. (π ≈ 3,23)

Arean på en cirkel är lika med arean på en kvadrat vars sida är 1/4 av cirkelns omkrets. (π = 4)

Lagförslaget skickades på remiss till den delstatliga utbildningskommittén som rekommenderade att det skulle godkännas. Av en slump råkade en professor C. A. Waldo dock befinna sig i Indianapolis vid tillfället, och lyckades efter att ha fått reda på förslaget övertala kommittén att rösta ner det. Lagstiftande församlingen har sedan aldrig tagit upp ärendet, och slipper därigenom att ta ställning till förslaget. Se vidare en:Indiana Pi Bill.

År 1998 spreds uppgifter på Internet om att delstaten Alabama skulle ha lagfäst π:s värde till det "bibliska värdet" 3,0. Nyheten var i själva verket ett aprilskämt som parodierade ovan nämnda fall samt kreationisters försök att i New Mexico motarbeta undervisningen om evolutionsteorin. Artikeln skrevs av en fysiker vid namn Mark Boslough.

π-kultur

Populärkultur

Talet π är ett av få matematiska objekt som regelbundet dyker upp i populärkulturen.

Framför allt har ett flertal science fiction-författare hänvisat till talet och dess fysikaliska eller metafysiska implikationer. Arthur C. Clarke och Stephen Baxter beskriver exempelvis i Time's Eye en värld skapad av utomjordingar där en sfär har omkrets–diameter-förhållandet 3, och i Eon av Greg Bear utnyttjas π för att beräkna rymdens krökning. I Carl Sagans roman Contact, som även filmatiserats, upptäcker huvudkaraktären att ett meddelande från universums skapare finns invävt i π – synligt då talet uttrycks i basen 11.

I Star Trek-avsnittet Wolf in the Fold tar ett ondskefullt väsen över rymdskeppets dator, med vars hjälp det hotar att förgöra besättningen. Spock beordrar då datorn att med högsta prioritet "beräkna π till den sista decimalen", vilket försätter den i en oändlig loop som gör den obrukbar för fienden. Omvänt utbrister professor Frink i ett avsnitt av The Simpsons att "π är exakt 3!" för att få full uppmärksamhet i ett rum fyllt av vetenskapsmän.

Sångerskan Kate Bush sjunger på sitt album Aerial en låt med titeln "π", vars text består av mer än 100 decimaler av π. Hennes fans har dock noterat att flera av decimalerna är felaktiga. Matte Matik hade då redan spelat in sin "Decimaler på pi", och även han gör fel och tappar bort sig "någonstans mellan 75 och 85"^[3].

Det finns också en film med titeln π, regisserad av Darren Aronofsky, som behandlar sambandet mellan tal och naturen.

Anhängare

Beundrare av talet π brukar uppmärksamma den 14 mars som π-dagen (03-14) och 22 juli som π-approximationsdagen (eftersom 22/7 är en bra approximation, till och med något bättre än 3,14).

Det har blivit en tävling att kunna memorera så många siffror av π som möjligt. Ett halvseriöst ämnesområde, känt som pifilologi, behandlar användandet av minnesregler för att memorera π.

Det finns en rekordlista för pi-memoreringar. Där finns under NEWS ett verifierat rekord av Chao Lu från Kina som den 20 november 2005 ur minnet lyckades räkna upp π med 67.890 decimaler. Dessutom finns ett overifierat rekord av japanen Akira Haraguchi som, 60 år gammal den 3 oktober 2006, lyckades räkna upp de första 100.000 decimalerna i π. Han slog med detta sitt gamla världsrekord från 2005 på 83 431 decimaler.

Daniel Tammet har ett såkallat savant-syndrom och har memoriserat pi till 22.514 decimaler. Han rabblade upp alla siffror korrekt på 5:09:24. "Det tog några veckor att lära sig!" sa han efteråt. En annan savant är Rüdiger Gamm. Han har lagt 5000 decimaler på minnet.

Nobelpristagaren i fysik Richard Feynman, känd för sitt intresse för huvudräkning, anmärkte en gång att han ville memorera π till den 767:e decimalen. Anledningen är att decimalerna 762 till och med 767 samtliga är nior, och att han då skulle kunna avsluta uppräkningen med "...nio, nio, nio, nio, nio, nio, och så vidare."

Pi – det fantastiska talet, är en bok (författare David Blatner, 1997) med fakta och anekdoter om π från alla tider; ISBN 91-7738-482-2. Bokens engelska original heter The Joy of Pi och har en egen hemsida för pi-fantaster. I boken finns ett kapitel om de ovannämnda bröderna Chudnovsky som inte bara fann nya formler för pi-beräkning, utan dessutom hemmabyggde en egen superdator med gigaflop-prestanda .

Här en länk till π med 49980 decimaler.

Se även

e (tal)

Referenser

[0] "A Trillion Pieces of Pi" - Mathematical Association of America 2002-12-16

[1] "A Trillion Pieces of Pi" - Mathematical Association of America 2002-12-16

[2] Matte Matiks hemsida

[1]

[2]

[3]

Pi