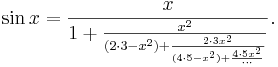Kedjebråk
Från Rilpedia
Ett kedjebråk är ett matematiskt uttryck på formen
där a0 är ett heltal och övriga an är positiva heltal. Samma kedjebråk kan mer koncist skrivas
Varje reellt tal kan representeras som ett kedjebråk. Kedjebråksframställning är en mer "naturlig" metod att representera tal än positionssystem och särskilt det decimala talsystemet, eftersom systemet inte är beroende av en godtyckligt vald talbas.
En viktig egenskap hos systemet är att de rationella talen precis motsvaras av ändliga kedjebråk. Även andra egenskaper kan utläsas från ett tals kedjebråksrepresentation; exempelvis motsvarar kedjebråk som upprepar sig precis de irrationella rötterna till kvadratiska ekvationer.
Några exempel på kedjebråk för matematiska konstanter är
- Gyllene snittet, φ = [1; 1, 1, 1, 1, ...]
- Roten ur två, √2 = [1; 2, 2, 2, 2, ...]
- Eulers tal, e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, ...]
- Pi, π = [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, ...]
Både e och π är transcendenta tal, men bara det förstnämnda talets kedjebråk uppvisar ett mönster.
Trunkering av kedjebråk är ett effektivt sätt att approximera irrationella tal. De första 1, 2, 3 respektive 4 termerna i kedjebråket för π ger exempelvis närmevärdena 3, 22/7, 333/106 och 355/113. Att 355/113 är en särskilt bra approximation för π förklaras av att nästa term i kedjebråket (292) är stor.
Även funktioner kan representeras med kedjebråk. Exempelvis ges sinus av
Här tillåts x vara något annat än ett heltal.
En märkvärdig egenskap hos kedjebråk är att termernas geometriska medelvärde är detsamma för nästan alla reella tal. Detta tal kallas Khinchins konstant och har värdet K ≈ 2,6854520010.




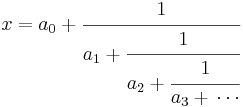
![x = [a_0; a_1, a_2, a_3, \ldots].\;](/w/images/sv.rilpedia.org/math/9/8/1/981a625c1c9300dde43ecb0b3dc3aabd.png)