Positionssystem

Från Rilpedia

Texten från svenska Wikipedia

Ett positionssystem är en typ av talsystem där talvärdet av en sifferföljd inte bara bestäms av siffrornas tilldelade värden utan även av deras positioner i följden. Det vanliga sättet att skriva tal på, det decimala talsystemet med arabiska siffror, är ett positionssystem.

Varje siffra anger antal av en potens av systemets talbas. Varje position har en bestämd potens och talets värde erhålles genom att multiplicera siffror med sina potenser och därefter addera dem ihop.

Innehåll

1 Introduktion
2 Allmänt om olika bassystem
3 Heltal i andra baser
4 Decimaltal i andra baser
- 4.1 Exempel: Decimaltal
- 4.2 Exempel: Decimaltal
5 Räkneoperationer i andra baser
6 Positionssystem
7 Andra talsystem

Introduktion

Låt oss titta på talet 3526. Vilket antal är detta? Skulle vi gå till banken och begära denna summa pengar så skulle vi få precis tre stycken tusenlappar, fem hundralappar, två tiokronor och sex enkronor. Vi kan skriva det som 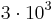$3\cdot 10^3$ -mynt, $5\cdot 10^2$ -mynt, $2\cdot 10^1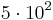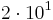$ -mynt plus 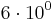$6\cdot 10^0$ -mynt.

Att vi just använder potenser av 10 för att representera tal kallas att vi normalt använder 10-bassystemet.

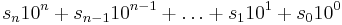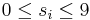Ett heltal i 10-systemt kan vi alltså skriva som $s_n10^n+s_{n-1}10^{n-1}+\dots+ s_1 10^1 + s_0 10^0$ , där $0\leq s_i \leq 9$ .

Antalet 23 kan vi skriva som 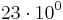$23\cdot 10^0$ , men vi vill ju att talet framför skall vara en enda siffra, så vi skriver det som 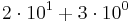$2\cdot 10^1 + 3\cdot 10^0$ . Motsvarande kommer att gälla i andra baser, vilket vi kommer att se strax.

Allmänt om olika bassystem

Hur ett tal beskrivs i bas $b$
Notation i bas $b$ :	$s 4$	$s 3$	$s 2$	$s 1$	$s 0$
Positionsvärde:	$b 4$	$b 3$	$b 2$	$b 1$	$b 0$
Talets värde:	$s 4 b 4 + s 3 b 3 + s 2 b 2 + s 1 b 1 + s 0 b 0$

Det enda som är speciellt med just det vanliga 10-bassystem är att vi baserar det på potenser av 10. Skulle vi inte kunna använda något annat tal, till exempel 5? Eller allmänt, $b$ . I rutan till höger ser vi då hur vi skulle uttrycka ett tal i bas $b$ .

För att ange vilken bas ett tal är skrivet i, så skriver vi basen med nedsänkt tal efter representationen. Till exempel så kan vi förtydliga talet $513$ genom att skriva det som $51310$ . Från och med nu så antas ett tal vara i 10-systemet om det saknar basangivelse.

Siffrorna som används i en bas $b$ är alltid 0 till $b - 1$ , eftersom vi på samma sätt som i 10-bassystemet kan växla till nästa valör; 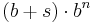$(b+s)\cdot b^n$ kan skrivas om till 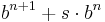$b^{n+1}+s\cdot b^n$ där $s < b$ .

Om vi skriver ett tal i bas $b$ , så är varje siffra i det talets representation mindre än $b$ .

Heltal i andra baser

Notation i bas 2:	1	1	1	0	0
Positionsvärde:	$24$	$23$	$22$	$21$	$20$
Talets värde:	16+8+4+0+0

Vi skall nu titta på $111002$ Använder vi vår "växlingstabell" så får vi att detta representerar talet 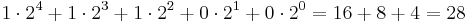$1\cdot 2^4 + 1\cdot 2^3 + 1\cdot 2^2 + 0\cdot 2^1 + 0\cdot 2^0 = 16+8+4 = 28$ . $111002$ är alltså talet $2810$ .

I högre baser än 10 uppstår ett problem. Låt oss titta på $12213$ . Är det 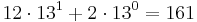$12\cdot 13^1 + 2\cdot 13^0 = 161$ , eller är det 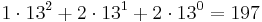$1\cdot 13^2 + 2\cdot 13^1 + 2\cdot 13^0 = 197$ ? För att beteckna tal i en högre bas än 10, så måste vi alltså ha fler siffror än 10, eller en annan lösning. Det vi gör är att gruppera siffrorna tydligare. $[12,2] 13$ är då det första talet, som är representationen av $161$ i bas 13. $[1,2,2] 13$ är då representationen för talet 197.

Ett alternativ är att fortsätta våra 10 siffror med bokstäver, så $A = 10$ , $B = 11$ , och så vidare. $[13,15] 16$ skulle då bli $C F 16$ . Detta skrivsätt används flitigt inom datalogivärlden, speciellt när man programmerar, då datorn internt arbetar i bas 2.

Exempel: Konvertering av tal till bas 10

Skriv talet $63427$ i bas 10

Vi skriver upp talet enligt mallen och vi beräknar ganska enkelt vad talet blir i bas 10.

Notation i bas 7:	6	3	4	2
Positionsvärde:	$73$	$72$	$71$	$70$
Talets värde:	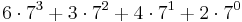$6\cdot 7^3+3\cdot 7^2+4\cdot 7^1+2\cdot 7^0$

$63427$ är då 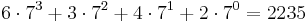$6\cdot 7^3 + 3\cdot 7^2 + 4\cdot 7^1 + 2\cdot 7^0 = 2235$ .

Exempel: Konvertering av tal till bas 10

Skriv talet $[14,2,70] 81$ i bas 10

Vi använder växlingstabellen och skriver upp

Notation i bas 81:	14	2	70
Positionsvärde:	$812$	$811$	$810$
Talets värde:	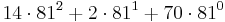$14\cdot 81^2+2\cdot 81^1+70\cdot 81^0$

Vi får då att talet är 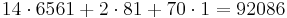$14\cdot 6561 + 2\cdot 81 + 70\cdot 1 = 92086$ .

Exempel: Konvertering av tal från bas 10

Skriv talet $15410$ i bas 16?

Vi tänker oss att vi har 154 enkronor på bordet framför oss, och vill växla till mynt med valörerna 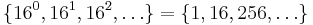$\{16^0,16^1,16^2,\dots\} = \{1,16,256,\dots\}$ . Vi ser 256-mynten är för stora, så det räcker med 16-mynten och 1-mynten. Hur många 16-mynt kan vi då tänkas behöva?

Jo, 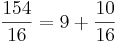$\frac{154}{16} = 9+\frac{10}{16}$ så 154 räcker till 9 hela 16-kronorsmynt. De resterande mynten får då vara kvar som enkronor. Alltså kan vi växla 154 enkronor till $9\cdot 16^1 + 10\cdot 16^0 = [9,10]$ .

Exempel: Konvertering av tal från bas 10

Skriv talet $163210$ i bas 3?

Vi har 1632 enkronor, och vill växla dessa till mynt i valörerna 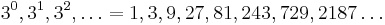$3^0,3^1,3^2,\dots = 1,3,9,27,81,243,729,2187\dots$

Samma princip som ovan ger oss då att

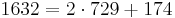$1632 = 2\cdot 729 + 174$ (vi växlar först 1458 mynt till 2 stycken 729-sedlar).

Forsätter vi nu växla mynt, så får vi då

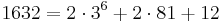
$1632 = 2\cdot 3^6 + 2\cdot 81 + 12$

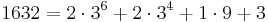
$1632 = 2\cdot 3^6 + 2\cdot 3^4 + 1\cdot 9 + 3$

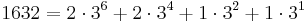
$1632 = 2\cdot 3^6 + 2\cdot 3^4 + 1\cdot 3^2 + 1\cdot 3^1$

Skriver vi då det som en summa av alla mynttyper så får vi 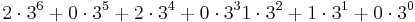$2\cdot 3^6 +0\cdot 3^5+ 2\cdot 3^4 +0\cdot 3^3 1\cdot 3^2 + 1\cdot 3^1 + 0\cdot 3^0$ .

Läser vi nu av antalet mynt av varje sort får vi $20201103$ . Alltså gäller $163210 = 2020110 3$

Decimaltal i andra baser

Hittills har vi bara tittat på hur heltal blir i andra baser. Nu skall vi behandla även icke-heltal. Det fungerar på precis samma sätt som när vi hade 10-öresmynt och 1-öresmynt, (som motsvarar $10 - 1$ -kronorssmynt och $10 - 2$ -kronorsmynt).

I dessa fall är det inte ovanligt att man får en oändlig decimalutveckling, vilket vi skall se i följande exempel:

Exempel: Decimaltal

Skriv talet $1,5 10$ i 3-bas.

De valörer vi skall växla till den här nu är 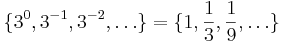$\{3^0,3^{-1},3^{-2},\dots\} = \{1,\frac{1}{3},\frac{1}{9},\dots\}$ .

Vi kan då säga att vi har två högar, en med mynt i bas 10, och en med mynt i bas 3. Genom att successivt växla från den ena högen till den andra genom att flytta största möjliga valör så får vi följande:

Antal i bas 10	Antal i bas 3
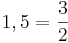$\displaystyle{1,5 = \frac{3}{2}}$	$0$
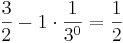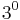$\displaystyle{\frac{3}{2}-1\cdot \frac{1}{3^0} = \frac{1}{2}}$	$\displaystyle{3^0}$
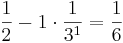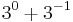$\displaystyle{\frac{1}{2}-1\cdot \frac{1}{3^1}= \frac{1}{6}}$	$\displaystyle{3^0+3^{-1}}$
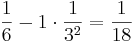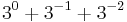$\displaystyle{\frac{1}{6}-1\cdot \frac{1}{3^2} = \frac{1}{18}}$	$\displaystyle{3^0+3^{-1}+3^{-2}}$
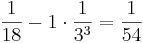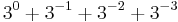$\displaystyle{\frac{1}{18}-1\cdot \frac{1}{3^3} = \frac{1}{54}}$	$\displaystyle{3^0+3^{-1}+3^{-2}+3^{-3}}$
$\dots$	$\dots$

Fortsätter vi oändligt länge, så ser vi att 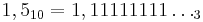$1,5_{10} = 1,11111111\dots_3$ . Talet $1,5$ har alltså oändlig decimalutveckling i bas 3.

Exempel: Decimaltal

Skriv talet $12,5 10$ i 4-bas.

Vi gör på samma sätt som i förra exemplet:

Antal i bas 10	Antal i bas 4
$12,5$	$0$
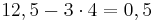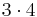$12,5-3\cdot 4 = 0,5$	$3\cdot 4$
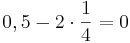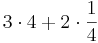$0,5 - 2\cdot \frac{1}{4} = 0$	$3\cdot 4 + 2\cdot \frac{1}{4}$

Här tog det slut mycket snabbare och vi konstaterar att 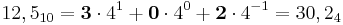$12,5_{10} = \mathbf{3}\cdot 4^1 + \mathbf{0}\cdot 4^0 + \mathbf{2}\cdot 4^{-1} = 30,2_4$

Räkneoperationer i andra baser

Man kan utföra de vanliga räknesätten i andra positionssystem precis som i bas 10.

Exempel: Att addera två tal i en annan bas

Utför additionen 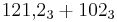$121,\!2_3 + 102_3$ .

Vi adderar siffrorna var för sig precis som med vanlig addition, med undantaget att $13 + 1 3 + 1 3 = 10 3$ .

Värde	$33$	$32$	$31$	$30$	$3 - 1$

Minne	1	1	1
Tal 1		1	2	1,	2
Tal 2		1	0	2,	0

Summa	1	0	0	0,	2

Svaret blir alltså 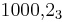$1000,\!2_3$ .

Exempel: Subtrahera två tal i en annan bas

Beräkna $[3,0,12,5] 14 - [1,9,1,4] 14$

Här ställer vi upp en tabell som med vanlig subtraktion, och som vanligt så får man "låna" från nästa siffra om man måste dra ett större tal från ett mindre.

(Att dra 11 enkronor från 1 enkrona och 3 stycken 14-kronor löses ju genom att man växlar en 14-krona till enkronor, och på liknande sätt för större valörer givetvis.)

Värde	$143$	$142$	$141$	$140$

Minne		14
Tal 1	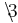$3\!\!\!\!\backslash$	0	12	5
Tal 2	1	9	1	4

Differens	1	5	11	1

Så svaret blir $[1,5,11,1] 14$ .

Exempel 3: Multiplicera två tal i en annan bas

Utför multiplikationen talen 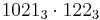$1021_3 \cdot 122_3$

Vi ställer upp för multiplikation:

Värde	$36$	$35$	$34$	$33$	$32$	$31$	$30$

				1	0	2	1
			$\cdot$		1	2	2

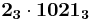$\mathbf{2_3\cdot 1021_3}$				2	1	1	2
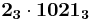$\mathbf{2_3\cdot 1021_3}$			2	1	1	2
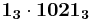$\mathbf{1_3\cdot 1021_3}$	+	1	0	2	1

Nu måste vi ju utföra additionen så det gör vi extra tydligt här med minnessiffror. Kom ihåg att $13 + 2 3 = 10 3$ .


Minne		1	2	1	1
				2	1	1	2
			2	1	1	2	0
	+	1	0	2	1	0	0

Summa		2	1	0	1	0	2

Alltså gäller det att 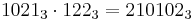$1021_3 \cdot 122_3 = 210102_3$