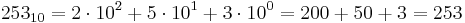Oktala talsystemet
Från Rilpedia
Det oktala talsystemet fungerar med samma princip som det decimala. Skillnaden är att i stället för 10 som talbas används 8.
Innehåll |
Decimala talsystemet
Antal siffror som används är 10: {0,1,...,9}.
Oktala talsystemet
Samma decimala tal 253 blir:
Antal siffror som används är 8: {0,1,...,7}.
Oktalkomma
Siffrorna till höger om oktalkommat är i negativ potens av 8.
Användning av det oktala talsystemet
Yuki-språket i Kalifornien och Pame-språket i Mexico använder oktala system, vilket kan förstås så att man ursprungligen räknat mellanrummet mellan fingrarna (åtta) istället för att räkna själva fingrarna (tio).
Swedenborgs system
År 1716 vände sig Karl XII till Emanuel Swedenborg med en begäran om ett praktiskt användbart talsystem med basen 64. Swedenborg avrådde från en så stor bas, med motiveringen att den vore svår att använda för personer med ringare fattningsförmåga än kungens. Han föreslog istället basen 8. Han utvecklar denna idé i ett två år därefter skrivet men ej offentliggjort manuskript: "En ny rekenkonst som växlas wid 8 i stelle then vahnliga wid talet 10". Siffrorna 0-7 betecknades med bokstäverna o, l, s, n, m, t, f och u (v). De används i ett positionssystem med entalssiffran sist. Talet 8 skrivs då "lo", 16 blir "so", 24 blir "no" och så vidare. Det första trebokstaviga talet 64 är "loo".
För att uttala dessa tal inskjutes en vokal mellan konsonanterna, ett a efter den första konsonanten, ett e efter den andra, sedan i, o, u och y. Det gör att man genom att bara lyssna på den sista stavelsen får grepp om talets storleksordning.
I skriften demonstrerars hur man kan räkna addition, subtraktion, multiplikation och division med dessa talbeteckningar, hur man kan konvertera mellan oktal och decimal beteckning, och där ges räknestickor för napierska logaritmer.
Swedenborgs system fick aldrig någon praktisk användning.
Data
Idag används det oktala talsystemet med vanliga sifferbeteckningar 0-7 i datorsammanhang, eftersom 8 är lika med 23, och 3 bitar sammanfattas i en oktal siffra. Det används inte så mycket, utan det hexadecimala talsystemet är det som används mest för att beskriva bitmönster.