Stone-Weierstrass sats
Från Rilpedia
Inom matematiken -- mer specifikt inom matematisk analys -- är Stone-Weierstrass teorem ett viktigt resultat som rör approximation av kontinuerliga funktioner.
Den klassiska varianten av satsen, kallad Weierstrass approximationssats, visades först av Karl Weierstrass år 1885 och säger att det, för varje kontinuerlig funktion
går att finna en sekvens 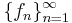 av polynom
av polynom
som konvergerar likformigt mot funktionen f.
Weierstrass approximationssats generaliserades senare av Marshall Stone, som visade ett liknande resultat för kontinuerliga funktioner definierade på ett godtyckligt kompakt Hausdorffrum. (Det slutna och begränsade intervallet [0,1] är ett exempel på ett kompakt Hausdorffrum.) Stone-Weierstrass teorem visar även att man kan approximera kontinuerliga funktioner med andra funktioner än polynom.
Weierstrass ursprungliga resultat lyder som följer:
Låt ![f : [0,1] \longrightarrow \mathbb{R}](/w/images/sv.rilpedia.org/math/6/0/4/604d545675decbffb29f00f727467861.png) vara en kontinuerlig funktion. Det existerar en sekvens
vara en kontinuerlig funktion. Det existerar en sekvens 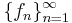 av polynom
av polynom ![f_n :
[0,1]\longrightarrow \mathbb{R}](/w/images/sv.rilpedia.org/math/6/4/f/64f614437d026a144fdc6ca12eb3c77f.png) som är sådana att
som är sådana att
En nackdel med Weierstrass approximationssats är att den endast garanterar existensen av approximerande polynom. Det finns emellertid ett bevis av satsen som ger en explicit konstruktion av sekvensen 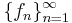 . Detta bevis, som ges nedan, är ett exempel på hur man kan använda sannolikhetsteori för att bevisa resultat inom matematisk analys.
. Detta bevis, som ges nedan, är ett exempel på hur man kan använda sannolikhetsteori för att bevisa resultat inom matematisk analys.
Sannolikhetsteoretiskt bevis av Weierstrass approximationssats
Vi börjar med att konstruera en sekvens 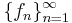 av polynom; de så kallade Bernsteinpolynomen. Därefter visar vi att de fyller sin funktion.
av polynom; de så kallade Bernsteinpolynomen. Därefter visar vi att de fyller sin funktion.
Välj ett godtyckligt heltal 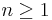 och ett godtyckligt tal
och ett godtyckligt tal ![p \in[0,1].](/w/images/sv.rilpedia.org/math/c/e/6/ce6af77c769679ef17b2a61d6387d04b.png) Låt
Låt
vara oberoende, diskreta, stokastiska variabler, alla med samma frekvensfunktion:
Summan av dessa stokastiska variabler är en diskret stokastisk variabel, 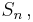 vars frekvensfunktion är
vars frekvensfunktion är
där heltalet 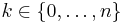 och symbolen
och symbolen 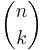 är en så kallad binomialkoefficient.
är en så kallad binomialkoefficient.
Kvoten Sn / n antar värden som ligger i intervallet [0,1], vilket innebär att vi kan applicera funktionen f på dessa värden. Detta ger upphov till en diskret stokastisk variabel, 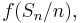 som antar värden ur mängden
som antar värden ur mängden 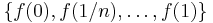 . Väntevärdet för denna stokastiska variabel är det reella talet
. Väntevärdet för denna stokastiska variabel är det reella talet
Den kända frekvensfunktionen för summan Sn låter oss uttrycka väntevärdet som
Funktionen ![f_n : [0,1] \longrightarrow \mathbb{R},](/w/images/sv.rilpedia.org/math/d/7/c/d7c2fc1662a20f78ee4ec38e91147c10.png) definierad av
definierad av
är ett polynom av grad n. Detta polynom kallas för Bernsteinpolynomet av grad n, associerat med funktionen f.
Eftersom heltalet 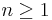 valdes godtyckligt, har vi härmed lyckats konstruera en sekvens
valdes godtyckligt, har vi härmed lyckats konstruera en sekvens 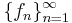 av polynom.
av polynom.
De tre första Bernsteinpolynomen är:
Vi skall nu visa att sekvensen av Bernsteinpolynom konvergerar likformigt mot funktionen f, vilket, med vår konstruktion av Bernsteinpolynomen som väntevärden av en sekvens av stokastiska variabler 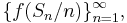 innebär att gränsvärdet
innebär att gränsvärdet
För att göra detta väljer vi ett godtyckligt tal ![p\in[0,1]](/w/images/sv.rilpedia.org/math/5/5/0/550abf67410399d394e58560a62f657a.png) och visar att
och visar att
där 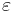 är ett godtyckligt valt positivt tal och δ(ε) är ett positivt tal som bara beror på talet
är ett godtyckligt valt positivt tal och δ(ε) är ett positivt tal som bara beror på talet 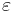 och inte på talet
och inte på talet ![p\in[0,1]](/w/images/sv.rilpedia.org/math/5/5/0/550abf67410399d394e58560a62f657a.png) . Därmed är talet
. Därmed är talet
en övre begränsning till mängden av tal
Då är talet
större än den minsta övre begränsningen (supremum) till mängden M, det vill säga
Denna övre begränsning är giltig för varje val av heltalet 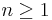 . Därför kan vi välja detta heltal så stort — större än ett visst heltal
. Därför kan vi välja detta heltal så stort — större än ett visst heltal 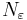 — att talet
— att talet
Då får vi resultatet att det för varje tal 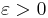 går att finna ett heltal
går att finna ett heltal 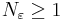 som är sådant att
som är sådant att
för varje heltal 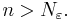 Detta är detsamma som att säga att
Detta är detsamma som att säga att
vilket i sin tur är samma sak som att säga att sekvensen av Bernsteinpolynom 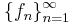 konvergerar likformigt mot den kontinuerliga funktionen f på intervallet [0,1].
konvergerar likformigt mot den kontinuerliga funktionen f på intervallet [0,1].
Det är endast en länk som fattas för att ovanstående resonemang skall bli korrekt: Vi måste visa att vi, för varje heltal 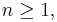 kan begränsa väntevärdet
kan begränsa väntevärdet
uppåt enligt
där 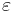 är ett godtyckligt valt positivt tal och δ(ε) är ett positivt tal som bara beror på talet
är ett godtyckligt valt positivt tal och δ(ε) är ett positivt tal som bara beror på talet 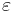 och inte på talet
och inte på talet ![p\in[0,1]](/w/images/sv.rilpedia.org/math/5/5/0/550abf67410399d394e58560a62f657a.png) .
.
Jensens olikhet tillämpad på den konvexa funktionen
låter oss begränsa väntevärdet uppåt med
Härnäst väljer vi ett godtyckligt reellt tal δ > 0 och splittrar upp väntevärdet
i en summa bestående av två termer, beroende på om den stokastiska variabeln
är större eller mindre än talet δ:
Eftersom funktionen
är kontinuerlig på det slutna och begränsade intervallet [0,1] så är den likformigt kontinuerlig på detta intervall och värdet
är ändligt.
Välj nu ett godtyckligt tal 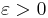 . Den likformiga kontinuiteten ger oss då ett tal
. Den likformiga kontinuiteten ger oss då ett tal 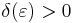 — som endast beror på talet
— som endast beror på talet 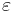 — som är sådant att, om
— som är sådant att, om
så är den stokastiska variabeln
Det är därför lämpligt att låta det tidigare godtyckligt valda talet talet δ vara just detta tal 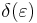 , vilket innebär att vi kan uppskatta det första väntevärdet i ovanstående summa enligt
, vilket innebär att vi kan uppskatta det första väntevärdet i ovanstående summa enligt
För att uppskatta den andra summan använder vi Triangelolikheten för reella tal och de faktum att
samt
för att få
där vi har använt oss av sambandet
mellan väntevärde och sannolikhet, giltigt för varje mätbar mängd A. (Mängden
är mätbar.)
Markovs olikhet låter oss uppskatta sannolikheten
enligt:
Eftersom väntevärdet för den stokastiska variabeln 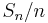 är
är
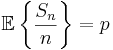 ,
,
så är väntevärdet
där ![\textrm{Var}\left[\frac{S_n}{n}\right]\,](/w/images/sv.rilpedia.org/math/7/5/b/75b610062a602eda7877c9fbb0cb7c4b.png) betecknar variansen för den stokastiska variabeln
betecknar variansen för den stokastiska variabeln 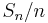 och kan beräknas exakt:
och kan beräknas exakt:
En kvadratkomplettering visar att det för varje värde på talet p gäller att
vilket låter oss uppskatta sannolikheten
enligt
Sammanfattningsvis har vi funnit den sökta övre begränsningen av väntevärdet
Därmed är beviset av Weierstrass approximationssats fullbordat.
Stone-Weierstrass teorem för komplex-värda funktioner
Låt X vara ett kompakt Hausdorffrum och låt 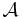 vara en sluten, komplex delalgebra till mängden
vara en sluten, komplex delalgebra till mängden 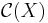 av alla komplex-värda kontinuerliga funktioner
av alla komplex-värda kontinuerliga funktioner 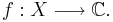 Om algebran
Om algebran 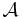 separerar punkter i X och är sluten under komplex-konjugering, så gäller endera av följande två fall:
separerar punkter i X och är sluten under komplex-konjugering, så gäller endera av följande två fall:
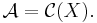
- Det finns en punkt
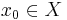 som är sådan att
som är sådan att
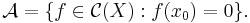
En delmängd 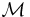 till mängden
till mängden 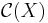 separerar punkter i X om det, för varje val av två distinkta punkter x och y i Hausdorffrummet X, går att finna en funktion
separerar punkter i X om det, för varje val av två distinkta punkter x och y i Hausdorffrummet X, går att finna en funktion 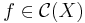 som skiljer på dessa punkter i den meningen att de komplexa talen f(x) och f(y) är olika.
som skiljer på dessa punkter i den meningen att de komplexa talen f(x) och f(y) är olika.
Stone-Weierstrass teorem medför Weierstrass resultat: Mängden av alla polynom på det kompakta Hausdorffrummet X är en delalgebra av de kontinuerliga funktionerna, eftersom summor och produkter av polynomer också är ett polynom. Vidare är den konstanta funktionen 1 ett polynom av grad 0 utan nollställe, och givet någon punkt x i ett intervall finns det polynom p,q sådana att 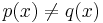 .
.
Stone-Weierstrass sats har stor betydelse inom många delar av den matematiska analysen.
Lokal-kompakt version av Stone-Weierstrass teorem
Det finns även en variant av Stone-Weierstrass teorem som gäller för lokalt kompakta Hausdorffrum som inte är kompakta.
Låt X vara ett lokal-kompakt Hausdorffrum som inte är kompakt och låt 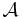 vara en sluten delalgebra av mängden
vara en sluten delalgebra av mängden 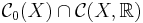 . Om mängden
. Om mängden 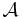 separerar punkter i X så gäller endera av följande två fall:
separerar punkter i X så gäller endera av följande två fall:
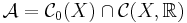 .
.- Det finns en punkt
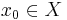 sådan att
sådan att
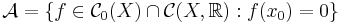 .
.
Mängden 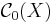 består av alla kontinuerliga funktioner
består av alla kontinuerliga funktioner
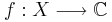
som försvinner i oändligheten, i den meningen att
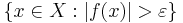
är en kompakt delmängd av X för varje val av det reella talet 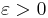 .
.



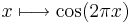 (heldragen kurva).
(heldragen kurva).![f:[0,1]\longrightarrow \mathbb{R},](/w/images/sv.rilpedia.org/math/b/8/a/b8a72333498dd82807d98f0c55f52c3a.png)
![\lim_{n\to\infty} \sup_{x\in[0,1]}\left\vert f(x) - f_n(x)\right\vert = 0.](/w/images/sv.rilpedia.org/math/3/c/5/3c54dd72baee77ce0458dc921201de6f.png)
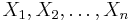
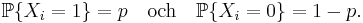
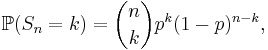
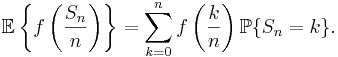
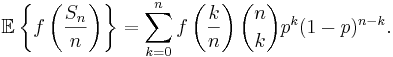
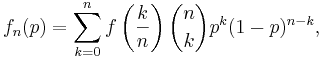
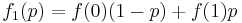
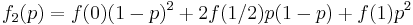
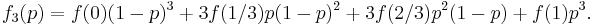
![\lim_{n\to\infty}\sup_{p\in[0,1]} \left\vert
\mathbb{E}\left\{f\left(\frac{S_n}{n}\right) - f(p)\right\}\right\vert = 0.](/w/images/sv.rilpedia.org/math/4/3/d/43d73f21e50bb38c00f3bb2822bd04a2.png)
![\left\vert \mathbb{E}\left\{f\left(\frac{S_n}{n}\right) -
f(p)\right\} \right\vert \leq \varepsilon + \max_{x\in[0,1]}\vert
f(x) \vert\frac{1}{2n\delta^2(\varepsilon)},](/w/images/sv.rilpedia.org/math/7/d/8/7d8ac1324da1944dbb619ff542575de0.png)
![\varepsilon + \max_{x\in[0,1]}\vert f(x)
\vert\frac{1}{2n\delta^2(\varepsilon)}](/w/images/sv.rilpedia.org/math/a/4/c/a4c280133fa59cdd9f4bb307d7e5125b.png)
![M = \left\{\left\vert
\mathbb{E}\left\{f\left(\frac{S_n}{n}\right) - f(p)\right\}
\right\vert : p \in [0,1]\right\}.](/w/images/sv.rilpedia.org/math/f/5/5/f557659d3ccb756ab1c4f31256aa3dae.png)
![\sup_{p\in[0,1]}\left\vert
\mathbb{E}\left\{f\left(\frac{S_n}{n}\right) - f(p)\right\}
\right\vert \leq \varepsilon + \max_{x\in[0,1]}\vert f(x)
\vert\frac{1}{2n\delta^2(\varepsilon)}.](/w/images/sv.rilpedia.org/math/b/3/f/b3fd2246e2040ba5422a7c85faab9649.png)
![\max_{x\in[0,1]}\vert f(x)
\vert\frac{1}{2n\delta^2(\varepsilon)} < \varepsilon.](/w/images/sv.rilpedia.org/math/6/6/d/66dc723add8fa962b3ca772d701908ff.png)
![\sup_{p\in[0,1]}\left\vert
\mathbb{E}\left\{f\left(\frac{S_n}{n}\right) - f(p)\right\}
\right\vert \leq 2\varepsilon,](/w/images/sv.rilpedia.org/math/e/7/b/e7b2f0f2e127d03d044d1dffb6b64010.png)
![\lim_{n\to\infty}\sup_{p\in[0,1]}\left\vert
\mathbb{E}\left\{f\left(\frac{S_n}{n}\right) - f(p)\right\}
\right\vert = 0,](/w/images/sv.rilpedia.org/math/a/1/0/a109f016d5af107b6b18fa8ff9e92c2f.png)
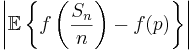
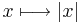
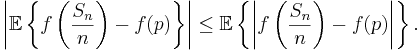
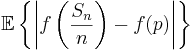
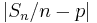
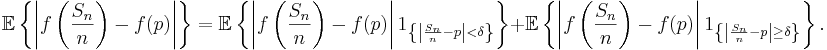
![\max_{x \in [0,1]} \vert f(x)\vert](/w/images/sv.rilpedia.org/math/7/1/d/71d6432f4ae64d60ecf140d80f3ac0e4.png)
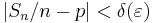
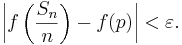
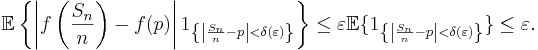
![\vert f(S_n/n) \vert \leq \max_{x\in[0,1]}\vert f(x)\vert](/w/images/sv.rilpedia.org/math/5/6/0/560691024c9dd8f44405b861cda4f4fb.png)
![\vert f(p) \vert \leq \max_{x\in[0,1]}\vert f(x)\vert,](/w/images/sv.rilpedia.org/math/5/0/4/50410a420b9d555e2b5baa803040626d.png)
![\mathbb{E}\left\{\left\vert f\left(\frac{S_n}{n}\right) -
f(p)\right\vert 1_{\left\{\left\vert \frac{S_n}{n} - p \right\vert
< \delta(\varepsilon)\right\}}\right\} \leq 2\max_{x\in[0,1]}\vert
f(x)\vert \mathbb{P}\left\{\left\vert \frac{S_n}{n} - p
\right\vert \geq \delta(\varepsilon)\right\},](/w/images/sv.rilpedia.org/math/b/c/f/bcfdf00e04d93f421b27eca9c2246612.png)

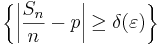
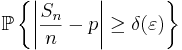
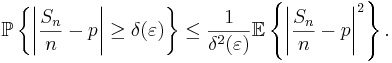
![\mathbb{E}\left\{\left\vert \frac{S_n}{n} - p
\right\vert^2\right\} =
\textrm{Var}\left[\frac{S_n}{n}\right],](/w/images/sv.rilpedia.org/math/f/4/9/f493e1873273487a6af4f9fae531e665.png)
![\textrm{Var}\left[\frac{S_n}{n}\right] = \frac{p(1-p)}{n}.](/w/images/sv.rilpedia.org/math/6/d/9/6d9793c1bac851b61fee997207032704.png)
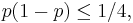
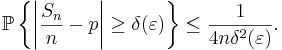
![\left\vert \mathbb{E}\left\{f\left(\frac{S_n}{n}\right) -
f(p)\right\} \right\vert \leq \varepsilon + \max_{x\in[0,1]}\vert
f(x) \vert\frac{1}{2n\delta^2(\varepsilon)}.](/w/images/sv.rilpedia.org/math/f/7/1/f71bfb4c4b08280704bc56113dabc902.png)