Sannolikhetsteori
Från Rilpedia
Sannolikhetsteorin är en matematisk disciplin som behandlar olika metoder för att beskriva och kvantifiera osäkerhet. Fundamenten för sannolikhetsteorin är Kolmogorovs axiom, mängdläran och kombinatoriken.
I synnerhet studeras utfall och händelser i ett utfallsrum, ofta i termer av sannolikhetsfördelningar.
Innehåll |
Klassisk sannolikhetsteori
Sannolikhetsteorin har sitt ursprung i 1500/1600-talets Italien och Frankrike där den tillämpades för hasardspel, den första läroboken skrevs av italienaren Gerolamo Cardano. Andra matematiker som gjort stora insatser för sannolikhetsteorin är Blaise Pascal, Thomas Bayes, Pierre de Fermat, Jakob Bernoulli, Abraham de Moivre och Pierre-Simon de Laplace.
Begrepp
Modern sannolikhetsteori
En problem med klassisk sannolikhetsteori är att man inte klassifierar händelser och sannolikhet med exakta matematisk koncept. När Georg Cantor formulerade mängdteori och Henri Lebesgue formulerade måtteori upptäckte en rysk matematiker Andrej Kolmogorov att man kan beskriva klassisk sannolikhetsteori med mängd- och måtteoretiska koncept, vilket ledde till sannolikhetsrummet.
Sannolikhetsrum
- Huvudartikel: Sannolikhetsrum
Det viktigaste begreppet inom modern sannolikhetsteori är det måtteoretiska begreppet sannolikhetsrum. Sannolikhetsrummet är en effektiv struktur eftersom man kan beskriva alla klassisk begrepp inom sannolikhet med det. Kolmogorov formulerade begreppet sannolikhetsrum med Kolmogorovs axiom:
- utfallsrummet är en mängd,
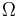 ,
, - händelser bildar en sigma-algebra,
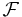 i
i 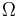 och
och - sannolikhet är ett mått,
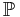 , definierad i
, definierad i 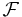 så att utfallsrummet har sannolikhet ett:
så att utfallsrummet har sannolikhet ett: 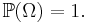
Tillämpningar
Sannolikhetsteori har många tillämpningar inom andra vetenskaper, exempelvis behöver fysik och statistik ofta sannolikhet med teoretiska aspekter.
Se även
Litteratur
- Olav Kallenberg, Probabilistic Symmetries and Invariance Principles. Springer -Verlag, New York (2005). 510 pp. ISBN 0-387-25115-4
- Olav Kallenberg Foundations of Modern Probability, 2nd ed. Springer Series in Statistics. (2002). 650 pp. ISBN 0-387-95313-2




