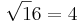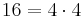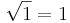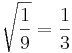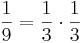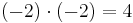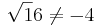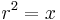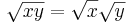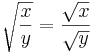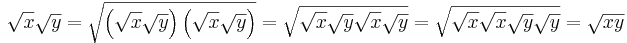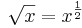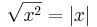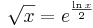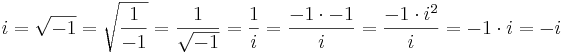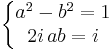Kvadratrot
Från Rilpedia
Kvadratrot är ett begrepp inom matematiken. Kvadratroten ur ett tal är det tal som multiplicerat med sig själv ger det första talet. Kvadratrot betecknas med ett rottecken, och till exempel så gäller för kvadratroten ur talet 16
eftersom
Vidare är till exempel
och
det senare eftersom
Med kvadratrötter menar man oftast positiva tal. Även om t ex
sägs då talet -2 inte vara en kvadratrot till 4, vilket däremot talet 2 är. Det förekommer dock att man talar om både 2 och -2 som kvadratrötter till talet 4. Rottecknet ger alltid det positiva talet:
Innehåll |
Formell definition
Kvadratroten av x är den ickenegativa lösningen r till ekvationen
där x är ett positivt reellt tal.
Att det finns sådana lösningar till alla positiva reella tal har inte alltid ansetts självklart, se till exempel kvadratroten ur två.
Kvadratroten ur negativa tal kan inte definieras på ett tillfredsställande sätt, men genom att införa de imaginära talen kan man finna lösningar till ekvationer av ovanstående typ även när x är negativt.
Mer allmänt kan kvadratrötter definieras för diverse objekt som exempelvis matriser, funktioner, och heltal under moduloräkning.
Positiva tal
Räknelagar
Följande egenskaper för kvadratrötter gäller för alla positiva reella tal x och y:
Dessa samband är ganska lätta att härleda; till exempel är
Dessutom gäller enligt definitionen av potens (se även potenslagarna) att
Ibland används följande samband mellan kvadratrot och absolutbelopp:
Kvadratroten ur ett positivt heltal n är ett heltal endast om n är ett kvadrattal, det vill säga för n = 1, 4, 9, 16, 25, .., och i annat fall ett irrationellt tal. Mer generellt är kvadratroten ur ett rationellt tal vars nämnare eller täljare inte är en perfekt kvadrat ett irrationellt tal. Kvadratroten ur 2, ungefär lika med 1,4142, var troligtvis det första kända irrationella talet, studerat av Pythagoreerna. Däremot är kvadratroten ur ett algebraiskt tal alltid algebraisk.
Beräkningsmetoder
Om exponential- och logaritmfunktionerna exp och ln finns tillgängliga kan kvadratrötter beräknas enligt
En effektiv algoritm för att approximera kvadratrötter, känd under namnet babyloniska metoden, är ett specialfall av Newton-Raphsons metod. För att beräkna 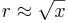 :
:
- Starta med ett godtyckligt värde rn (ju närmare roten, desto färre upprepningar behöver göras):rn
- ersätt r med medelvärdet av r och
 :
: 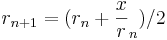
- om rn+1 - rn inte nått önskvard noggrannhetsgräns: gå till steg två igen
Beräkningskomplexiteten för den babyloniska metoden är densamma som för multiplikation.
Negativa och komplexa tal
För att kunna lösa ekvationen r2 = x där x är ett känt negativt tal har man infört imaginära tal (betecknas i) enligt definitionen i2 = − 1. Det visar sig då att man kan lösa alla typer av polynomekvationer. Även om det egentligen inte möjligt att använda rottecknet direkt, eftersom detta endast går att definiera entydigt för reella, postiva tal, används det dock ibland informellt.
- Exempel:
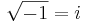 är inte ett korrekt skrivsätt, eftersom då följande skulle gälla
är inte ett korrekt skrivsätt, eftersom då följande skulle gälla
- Exempel: Låt
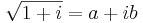 . Man vet att
. Man vet att 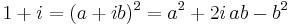 , enligt definitionen av kvadratrot och räkneregler för komplexa tal. Man kan nu identifiera konstanterna och få ekvationssystemet
, enligt definitionen av kvadratrot och räkneregler för komplexa tal. Man kan nu identifiera konstanterna och få ekvationssystemet
- Detta system har två lösningar och kräver således fler villkor för att vara entydigt.
Historik
Det äldsta kända exemplet på kvadratrotsberäkningar finns i den egyptiska Rhindpapyrusen från 1650 f.Kr.
Kvadratroten användes också i både det antika Kina och Indien. I Indien finns metoder för att beräkna närmevärden till kvadratrötter beskrivna på 500-talet f.Kr., i bland annat Baudhayanasutran. I Aryabhatas Aryabhatiya finns en metod för att beräkna kvadratroten ur tal med många siffor.
Den äldsta kände kinesiska matematiska texten Texter om beräkning är författad någon gång mellan 202 f.Kr. och 186 f.Kr., under den tidiga Handynastin. Där finns en metod beskriven för att finna närmevärden till kvadratrötter.
I Europa började man beräkna kvadratrötter på medeltiden. Symbolen  började användas på 1500-talet.
började användas på 1500-talet.
Alternativa representationer
Förkortningen sqrt (från engelskans square root) används inom olika programspråk som operator för kvadratrotsfunktionen. Vanligast är formatet: Sqrt(operand), men de flesta basicdialekter använder det något kortare SQR(x). Sqrt används även ofta i elektroniskt kodad text som ASCII eller Unicode då möjlighet att skriva ett kvadratrotstecken saknas och lånar då formatet mer eller mindre direkt från programspråket C.





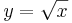 är en halv, liggande
är en halv, liggande