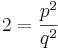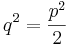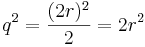Kvadratroten ur 2
Från Rilpedia
Roten ur 2 (egentligen kvadratroten ur 2) är i matematiken berömt då det ledde det antika Greklands matematiker till insikten att de rationella talen inte är tillräckliga i alla lägen. Om man har en kvadrat där längden av sidan är 1, så kommer diagonalens längd att bli roten ur 2.
Beviset för att roten ur 2 är irrationellt sägs ha varit särskilt besvärande för Pythagoras. Beviset är också ett klassiskt exempel på ett motsägelsebevis.
Bevis
Antag att roten ur 2 är rationellt. Det innebär att man kan skriva 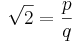 . Antag nu att kvoten p/q är maximalt förkortad (detta skrivs normalt sgd(p,q)=1). Detta kan göras utan att ändra på p/q:s egenskaper. Nu kvadrerar vi båda leden:
. Antag nu att kvoten p/q är maximalt förkortad (detta skrivs normalt sgd(p,q)=1). Detta kan göras utan att ändra på p/q:s egenskaper. Nu kvadrerar vi båda leden:
och flyttar runt:
Eftersom q2 är ett heltal, så måste 2 ingå som en primtalsfaktor i p2. Eftersom att jämna kvadrattal har jämna rötter ingår även 2 som en primtalsfaktor i p. Vi skriver därför att p=2r. Detta ger då
Genom att dividera båda led med 2 fås samma situation som ovan. Detta innebär att 2 även måste vara en primtalsfaktor i q, men vi hade antagit att sgd(p,q)=1, och har därför nått en motsägelse. Därför måste antagandet att roten ur 2 är rationellt vara falskt. Q.E.D.