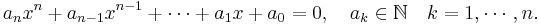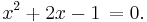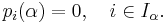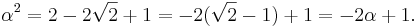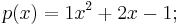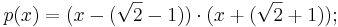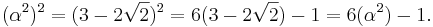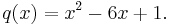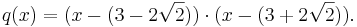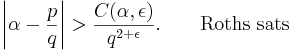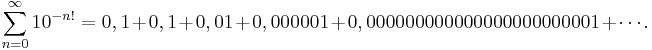Algebraiskt tal

Från Rilpedia

Texten från svenska Wikipedia

Inom matematik säger man att det komplexa talet x är algebraiskt om det är en lösning till någon polynom ekvation vars koefficienter är heltal:

$a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1 x + a_0 = 0, \quad a_k \in \N \quad k=1,\cdots,n.$

Exempelvis är 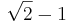$\sqrt{2} - 1$ ett algebraiskt tal, eftersom det är en lösning till följande polynomekvation vars koefficienter är heltal:

$x^2 + 2x - 1 \,= 0.$

Den centrala egenskapen är att polynomekvationernas koefficienter måste vara heltal.

Egenskaper

Alla rationella tal är algebraiska, men det finns reella tal som inte är algebraiska: Förhållandet mellan en cirkels omkrets och dess diameter, det vill säga talet $π$ , är inte ett algebraiskt tal.
Om ett algebraiskt tal är lösningen till en ekvation av grad n, men inte till någon ekvation av lägre grad, sägs talet vara ett algebraiskt tal av graden n.
De algebraiska talen bildar en uppräknelig mängd, till skillnad från de trancendenta talen. Dessa är de reella tal som inte är algebraiska; det finns alltså ingen polynomekvation, vars koefficienter är heltal, som har ett transcendent tal som lösning.

Exempel

Två exempel på transcendenta tal är e (basen för den naturliga logaritmen) och $π$ (förhållandet mellan en cirkels omkrets och dess diameter).

Algebraiska heltal

Låt $α$ vara ett algebraiskt tal. Då vet vi att det finns polynom med heltalskoefficienter för vilka talet $α$ är en rot:

$p_i(\alpha) = 0, \quad i \in I_\alpha.$

Indexmängden $I α$ är en icke-tom mängd av positiva heltal. Man kan visa att denna mängd innehåller ett speciellt index, $i 0$ , som motsvarar ett polynom 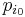$p_{i_0}$ av lägst grad ( 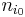$n_{i_0}$ ) bland polynomen 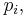$p_i,\,$ och som inte kan faktoriseras i en produkt av polynom med lägre grad än 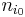$n_{i_0}$ . Om koefficienterna till det speciella polynomet 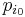$p_{i_0}$ är heltal, så säger man att $α$ är ett algebraiskt heltal och det speciella polynomet 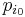$p_{i_0}$ kallas det algebraiska talets minimalpolynom.

Exempel

Vi skall visa att det positiva reella talet 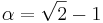$\alpha = \sqrt{2}-1$ är ett algebraiskt heltal. Till att börja med skall vi visa att det är ett algebraiskt tal:

$\alpha^2 = 2-2\sqrt{2}+1 = -2(\sqrt{2}-1)+1 = -2\alpha +1.$

Denna beräkning visar att talet $α$ är en rot till polynomet

$p(x) = 1x^2 + 2x - 1;\,$

Då detta polynom har koefficienter som är heltal (talen 1, 2 och -1) är roten $α$ ett algebraiskt tal.

Polynomet kan faktoriseras i en produkt av polynom vars grader är lägre än två:

$p(x) = (x-(\sqrt{2}-1)) \cdot (x+(\sqrt{2}+1));$

Men koefficienterna i de två polynomen är inte heltal; Av detta kan vi dra slutsatsen att $p (x)$ är minimalpolynomet associerat med det algebraiska talet 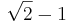$\sqrt{2}-1$ . Det faktum att ett minimalpolynom existerar, visar att 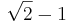$\sqrt{2}-1$ är ett algebraiskt heltal.

Om $n$ är ett positivt heltal (exempelvis 3), så är $n 2$ också ett positivt heltal. Vi skall undersöka om detta även gäller för algebraiska heltal; Som försöksobjekt väljer vi det algebraiska heltalet 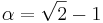$\alpha = \sqrt{2}-1$ och frågar oss om talet 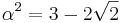$\alpha^2 = 3-2\sqrt{2}$ också är ett algebraiskt heltal?

För det första undersöker vi om det är ett algebraiskt tal:

$(\alpha^2)^2 = (3-2\sqrt{2})^2 = 6(3-2\sqrt{2}) - 1 = 6(\alpha^2)-1.$

Det reella talet $α 2$ är tydligen en rot till följande polynom vars koefficienter är heltal:

$q(x) = x^2-6x+1.\,$

Detta visar att talet $α 2$ är ett algebraiskt tal.

För det andra undersöker vi om det finns ett minimalpolynom associerat med det algebraiska talet $α 2$ . Polynomet q kan faktoriseras i en produkt med två polynom av lägre grad än två:

$q(x) = (x-(3-2\sqrt{2})) \cdot (x-(3+2\sqrt{2})).$

Koefficienterna för dessa polynom är inte heltal; Därför kan vi dra slutsatsen att q är ett minimalpolynom associerat med det algebraiska talet $α 2$ , vilket visar att $α 2$ är ett algebraiskt heltal.

Baserat på denna undersökning kan man fråga sig om följande regel gäller:

Om

β

är ett algebraiskt heltal, så är

β 2

också ett algebraiskt heltal.

En generalisering av detta påstående till andra heltalspotenser än två, är följande:

Om

β

är ett algebraiskt heltal och n är ett positivt heltal, så är

β n

ett algebraiskt heltal.

Båda dessa påståenden är sanna om följande påstående är sant:

Om

α

och

β

är algebraiska heltal, så är deras produkt 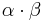$\alpha \cdot \beta$ också ett algebraiskt heltal.

Kardinalitet

Mängden av alla algebraiska tal är uppräknelig. Av detta följer att mängden av transcendenta tal är överuppräknelig, eftersom mängden av de reella talen R är överuppräknelig och
$\mathbb{R} = \{$ x: x är ett algebraiskt tal $\} \cup \{$ x: x är ett transcendent tal $\} \,$ .

Approximation av algebraiska tal

Enligt Abel-Ruffinis sats kan algebraiska tal av grad fem och högre generellt inte uttryckas i termer av ändligt många heltal, aritmetiska operationer, och rotutdragningar. Med andra ord: Det går inte att finna en allmän lösningsformel för femte- eller högregradsekvationer, om man kräver att denna lösningsformel skall bestå av ändligt många heltal som adderas, subtraheras, divideras, multipliceras eller tas roten ur.

Exempel på sådana formler är den allmänna lösningsformeln för andragradsekvationer och Cardanos formel för den allmänna tredjegradsekvationen.

Eftersom det finns effektiva numeriska metoder för att lösa polynomekvationer, kan dock alla algebraiska tal effektivt approximeras med rationella tal.

Emellertid gäller det att om $α$ är ett algebraiskt irrationellt tal och p och q är godtyckliga heltal och $ε$ ett positivt tal, så existerar det en konstant $C (α,ε)$ som gör att följande olikhet är uppfylld:

$\left\vert \alpha -\frac{p}{q}\right\vert > \frac{C(\alpha, \epsilon)}{q^{2+\epsilon}}. \qquad \text{Roths sats}$

Algebraiska irrationella tal kan alltså inte approximeras godtyckligt väl av rationella tal; denna egenskap kan användas för att visa att vissa tal inte är algebraiska. Genom att använda sig av ett svagare resultat än Roths sats lyckades Joseph Liouville visa att följande serie inte representerar ett algebraiskt tal:

$\sum_{n=0}^\infty 10^{-n!} = 0,1+0,1+0,01+0,000001+0,000000000000000000000001+\cdots.$

Se även

Olika typer av matematiska tal

Naturliga tal - Heltal - Positiva tal - Noll - Negativa tal - Rationella tal - Irrationella tal - Reella tal - Algebraiska tal - Transcendent tal - Imaginära tal - Komplexa tal - Hyperkomplexa tal (Kvaternioner Oktonioner Sedenioner) - Perfekta tal

Algebraiskt tal

Från Rilpedia

Innehåll

Egenskaper

Exempel

Algebraiska heltal

Exempel

Kardinalitet

Approximation av algebraiska tal

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk