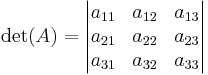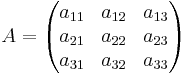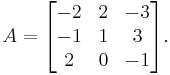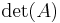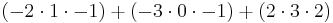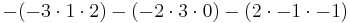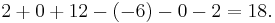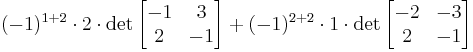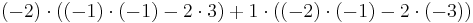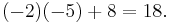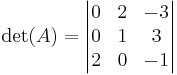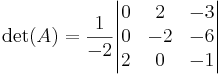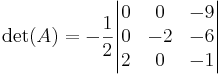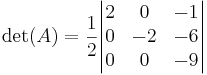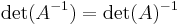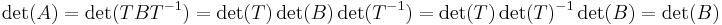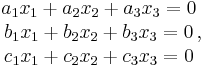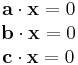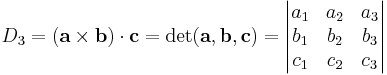Determinant

Från Rilpedia

Version från den 28 februari 2009 kl. 10.40 av 83.233.152.19 (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Determinant, en funktion som tillordnar en skalär för varje kvadratisk matris (matriser med lika antal rader och kolumner). I en geometrisk tolkning är determinanten av matris A skalfaktorn hos volymen av enhetskuben efter den linjära avbildningen som definieras av A har verkat på den. Den är även viktig inom matematisk analys, då den används vid variabelsubstitution (se jacobian).

Determinanten för en matris A tecknas det(A). Även notationen |A| används ibland men då den lätt förväxlas med beteckningen för norm och absolutbelopp är den ej att rekommendera. När man vill skriva determinanten för matrisen med alla element utskrivna används följande skrivsätt:

\det(A)=\begin{vmatrix}a_{11}& a_{12} & a_{13}\\ a_{21}& a_{22} & a_{23}\\ a_{31}& a_{32} & a_{33}\end{vmatrix}

Innehåll

Determinant för 2×2-matriser

matrisen 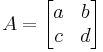A=\begin{bmatrix}a&b\\ c&d\end{bmatrix} har determinanten

det(A) = ad − bc.

Om matrisen har endast reella element kan determinanten tolkas som arean av parallellogrammet med hörn i (0,0), (a,c), (b,d) samt (a+b,c+d), multiplicerat med en teckenfaktor.

Determinant för 3×3-matriser

A=\begin{pmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{pmatrix}

har determinanten

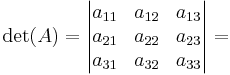
\det(A) = \begin{vmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}& a_{32}&a_{33}\end{vmatrix} =
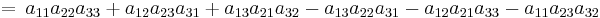=\,a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32}.

För 3×3-matriser kan Sarrus regel användas som minnesregel, enligt vilken man lägger till de två översta raderna under matrisen, och drar alla sex diagonaler med tre element och tar produkten av de element som står i samma diagonal. Dess produkter summeras sedan, med positivt tecken för de som går från vänster snett nedåt höger och negativt för de övriga.

Denna regel fungerar enbart för 3×3-matriser, och skall inte användas på andra.

Beräkning av determinanten

Determinanten kan beräknas på liknande sätt som vid Gausselimination och följande regler:

  1. Om A är en triangulär matris, alltså 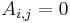A_{i,j} = 0 \, för alla i > j eller för alla i < j så är 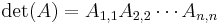\det(A) = A_{1,1} A_{2,2} \cdots A_{n,n} \, (produkten av A:s diagonalelement).
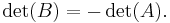
  2. Om matrisen B kan fås ur A genom att byta plats på två rader eller kolumner så är \det(B) = -\det(A). \,
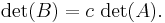
  3. Om matrisen B kan fås ur A genom att multiplicera en rad eller kolumn med skalären c, så är \det(B) = c\,\det(A). \,
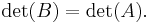
  4. Om matrisen B kan fås ur A genom att addera en multipel av en rad eller kolumn till en annan rad respektive kolumn så är \det(B) = \det(A). \,

Det man gör är alltså att man börjar med sin matris, omvandlar den till triangulär form med regel 2-4, varefter man använder regel 1.

Alternativt kan man Laplaceutveckling, det vill säga man går längs en rad eller kolumn:

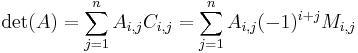\det(A) = \sum_{j=1}^n A_{i,j}C_{i,j} = \sum_{j=1}^n A_{i,j} (-1)^{i+j} M_{i,j} - går längs den i:e raden
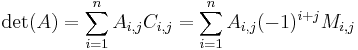\det(A) = \sum_{i=1}^n A_{i,j}C_{i,j} = \sum_{i=1}^n A_{i,j} (-1)^{i+j} M_{i,j} - går längs den j:e kolumnen

Ci,j är matrisens kofaktorer, alltså ( − 1)i + j gånger underdeterminanten, vilket är determinanten för den matris man får om man tar bort rad i och kolumn j från matrisen A.

Exempel

Vi skall beräkna determinanten av matrisen

A = \begin{bmatrix}-2&2&-3\\ -1& 1& 3\\ 2 &0 &-1\end{bmatrix}.

Vi kan göra detta direkt:

\det(A)\, =\, (-2\cdot 1 \cdot -1) + (-3\cdot 0 \cdot -1) + (2\cdot 3\cdot 2)
- (-3\cdot 1 \cdot 2) - (-2\cdot 3 \cdot 0) - (2\cdot -1 \cdot -1)
=\, 2 + 0 + 12 - (-6) - 0 - 2 = 18.\,

Vi kan även använda Laplaceutvecklingen längs en viss rad eller kolumn. Det är då smart att välja en rad eller kolumn med många nollor, så vi tar den andra kolumnen:

\det(A)\, =\, (-1)^{1+2}\cdot 2 \cdot \det \begin{bmatrix}-1&3\\ 2 &-1\end{bmatrix} + (-1)^{2+2}\cdot 1 \cdot \det \begin{bmatrix}-2&-3\\ 2&-1\end{bmatrix}
=\, (-2)\cdot((-1)\cdot(-1)-2\cdot3)+1\cdot((-2)\cdot(-1)-2\cdot(-3))
=\, (-2)(-5)+8 = 18.\,

Slutligen använder vi den Gausseliminationsliknande metoden. När man gör detta för hand är det ofta lätt att hitta genvägar, till exempel genom att använda Laplaceutvecklingen när endast en 2×2-determinant återstår, men för att illustrera metoden avstår vi från detta här. Vi börjar med att addera den andra kolumnen till den första, vilket inte påverkar determinanten

\det(A)=\begin{vmatrix}0&2&-3\\ 0 &1 &3\\ 2 &0 &-1\end{vmatrix}

Nu skalar vi om den andra raden med en faktor -2, vilket gör att vi även ändrar determinnanten med en faktor -2. Därför gäller

\det(A)=\frac{1}{-2}\begin{vmatrix}0&2&-3\\ 0 &-2 &-6\\ 2 &0 &-1\end{vmatrix}

Nu adderar vi den andra raden till den första

\det(A)=-\frac{1}{2}\begin{vmatrix}0&0&-9\\ 0 &-2 &-6\\ 2 &0 &-1\end{vmatrix}

Slutligen byter vi plats på den första och den tredje raden, och får då en triangulär form, samt ytterligare ett minustecken:

\det(A)=\frac{1}{2}\begin{vmatrix}2 &0 &-1\\ 0 &-2 &-6\\ 0&0&-9\end{vmatrix}

Nu är det lätt att räkna ut att 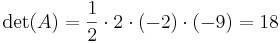\det(A)= \frac{1}{2}\cdot 2 \cdot (-2) \cdot (-9)=18

Egenskaper

Determinant-funktionen respekterar multiplikation.

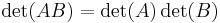\det(AB) = \det(A)\det(B) \, för alla n×n-matriser A och B.
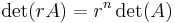\det(rA) = r^n \det(A) \, för alla n×n-matriser A och alla skalärer r.
\det(A^{-1}) = \det(A)^{-1} \,

Matrisen och dess transponat har samma determinant.

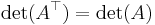\det(A^\top) = \det(A) \,.

Determinanten är invariant under basbyte. Om en matris A kan representas som matris B, dvs A = TBT − 1, så kan man skriva, med hjälp av reglerna ovan:

\det(A) = \det(TBT^{-1}) = \det(T) \det(B) \det (T^{-1}) = \det(T)\det(T)^{-1}\det(B) = \det(B)\,

Detta får även som följd att determinanten är produkten av egenvärdena för matrisen, dvs om A har egenvärdena λ1,...,λn:

det(A)= \lambda_1 ... \lambda_n \,

Vilket inses lätt för diagonaliserbara matriser. För icke diagonaliserbara matriser kan man använda Schurs sats, och få en triangulär matris som man utvecklar efter första kolonn hela tiden.

Användningsområden för determinanter

Determinanter används för att karakterisera matriser och att explicit beskriva lösningar för dess motsvarande linjära ekvationssystem. Om determinanten är noll har ekvationssystemet antingen oändligt många lösningar eller också ingen lösning alls. Är determinanten nollskild har ekvationssystemet en unik lösning. Determinanten kan även användas för att hitta egenvärdena för matrisen A via sekularekvationen det(A − λIn) = 0

Exempel

Determinanter uppstod av ett problem med linjära ekvationssystem,

\begin{matrix} a_1x_1+a_2x_2+a_3x_3 = 0 \\ b_1x_1+b_2x_2+b_3x_3 = 0 \\ c_1x_1+c_2x_2+c_3x_3 = 0 \end{matrix},

som består i att hitta icke-triviala lösningar (x1 ≠ 0, x2 ≠ 0, x3 ≠ 0) och under vilka förutsättningar dessa går att finna. (Jämför Cramers regel.)

Med a = (a1, a2, a3), b = (b1, b2, b3), c = (c1, c2, c3) och x = (x1, x2, x3), kan ovanstående ekvationssystem uttryckas i vektornotation:

\begin{matrix} \mathbf{a}\cdot\mathbf{x} = 0 \\ \mathbf{b}\cdot\mathbf{x} = 0 \\ \mathbf{c}\cdot\mathbf{x} = 0 \\ \end{matrix}

Geometriska tolkningen av ovanstående tre skalärprodukter är att x är ortogonal till samtliga vektorer a, b och c. Om volymen som spänns ut av dessa koefficientvektorer, d.v.s. trippelprodukten eller determinanten, av vektorerna a, b och c

D_3 = (\mathbf{a}\times\mathbf{b})\cdot\mathbf{c} = \det(\mathbf{a}, \mathbf{b}, \mathbf{c}) = \begin{vmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{vmatrix}

inte är noll, finns endast den triviala lösningen x = 0. Om så inte är fallet så är någon av koefficientvektorerna en linjärkombination av de övriga två. Säg att c är en linjärkombination av a och b. Detta innebär att x ∝ a×b vilket ger x·c = 0. I detta fall finns oändligt många lösningar på ekvationssystemet.

Historik

Determinater beräknades faktiskt innan begreppet "matris" fanns, och betraktades då som en egenskap hos linjära ekvationssystem, eftersom determinanten avgör (latin: determino) om systemet har en unik lösning. Determinanter för 2×2-matriser studerades av Gerolamo Cardano under 1500-talet, men begreppet introducerades århundradet efter av Gottfried Leibniz, som även studerade determinanter för större system. 1750 utvecklade Gabriel Cramer teorin.

1771 insåg Vandermonde (1771) att determinanten levde ett liv utanför ekvationssystemen. 1772 presenterade Pierre Simon de Laplace sin metod för expansion i underdeterminanter; Vandermonde hade då redan gett ett specialfall. Redan 1773 behandlade sedan Joseph Louis Lagrange andra och tredje ordningens determinanter, och han var även den förste att använda i andra sammanhang än elimination samt lyckades att visa flera specialfall av generella samband.

Carl Friedrich Gauss blev 1801 näste man att utvidga området. På samma sätt som Lagrange använde han flitigt determinanterna inom talteori, och var den förste att använda ordet determinant (Laplace hade använt resultant), även om det inte var i den nuvarande meningen.

Näste person på tur att ge betydande bidrag var Jacques Philippe Marie Binet, som 1811 och 1812 formellt gav resultatet om determinanten för produkten mellan två n × m-matriser (Cauchy-Binets formel), som för specialfallet n=m reduceras till multiplikationssatsen enligt ovan. Den 30 november 1812, när han presenterade sina resultat för akademin presenterade även Augustin Louis Cauchy vad han kommit fram till inom ämnet. Han blev då den förste att använda ordet determinant i sin moderna betydelse och lyckades summera och förenkla vad som var känt inom ämnet, och gav ett bättre bevis än det Binet presenterade.

1827 blev sedan Carl Gustav Jakob Jacobi näste viktige bidragsgivare, genom att använda den funktional-determinant som senare skulle bli känd under namnet Jacobian.

Hämtad från "https://sv.rilpedia.org/wiki/Determinant"
Personliga verktyg