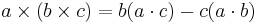Trippelprodukt

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Det finns två sorters trippelprodukter av vektorer; den skalära och den vektoriella. Båda handlar om att multiplicera tre vektorer (a,b,c) med varandra genom en serie skalär- och kryssprodukter.

Innehåll

Skalär trippelprodukt

Den skalära trippelprodukten definieras som skalärprodukten av den ena vektorn med kryssprodukten av de två andra, dvs: 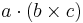a \cdot (b \times c)

Egenskaper

Vektorerna kan inom produkten flyttas runt cykliskt, dvs:

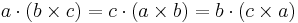
a \cdot (b \times c) = c \cdot (a \times b) = b \cdot (c \times a)

Geometrisk tolkning

Den skalära trippelprodukten kan geometriskt tolkas som volymen (med tecken) av parallellepipeden som definieras av de tre vektorerna.

Determinanttolkning

Man kan också tolka den skalära trippelprodukten som determinanten av den matris som har de tre vektorerna som rader eller kolonner.

Vektoriell trippelprodukt

Den vektoriella trippelprodukten är

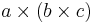
a \times (b \times c)

Egenskaper

Den vektoriella trippelprodukten kan utvecklas med hjälp av "BAC-CAB-regeln":

a \times (b \times c) = b(a\cdot c) - c(a\cdot b)

Hämtad från "https://sv.rilpedia.org/wiki/Trippelprodukt"
Personliga verktyg