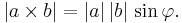Kryssprodukt

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Parallellogrammets area ger storleken av a×b

En kryssprodukt är en form av vektorprodukt som är definierad för vissa vektorrum. Kryssprodukten är en pseudovektor.

Innehåll

Kryssprodukten i R3

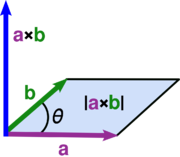
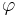Två tredimensionella vektorer (a och b) som kryssmultipliceras ger upphov till en ny tredimensionell vektor (a \times b). Som alla andra tredimensionella vektorer har kryssprodukten en längd och en riktning; dess riktning är vinkelrät mot det plan som spänns upp av de två vektorerna a och b, samt ordnad efter högerhandsregeln och dess längd är bestämd av vinkeln (\varphi) mellan dessa vektorer:

\vert a \times b \vert = \vert a \vert \, \vert b \vert \, \sin \varphi.

Längden av kryssprodukten kan tolkas som arean av ett parallellogram som spänns upp av de multiplicerade vektorerna. Kryssprodukten av två parallella vektorer blir alltså noll.

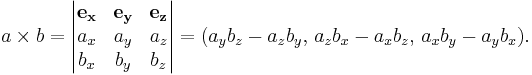
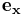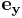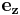Om man känner till de cartesiska komponenterna för två vektorer a och b, så kan man beräkna de motsvarande cartesiska komponenterna för kryssprodukten som en determinant: a \times b = \begin{vmatrix} \mathbf{e_x} & \mathbf{e_y} & \mathbf{e_z} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \\ \end{vmatrix} = (a_yb_z - a_zb_y, \, a_zb_x - a_xb_z, \, a_xb_y - a_yb_x).

där \mathbf{e_x}, \mathbf{e_y} och \mathbf{e_z} betecknar enhetsvektorerna i R3.

Fysikaliska tillämpningar

Kryssprodukten används för att beräkna vridmoment, magnetfält och andra vektorvärda storheter som är produkten av två fysikaliska vektorer.

Generaliseringar

Begreppet kryssprodukt kan generaliseras till att gälla vektorer a och b i högre dimensioner. Kryssprodukten är då en kombination av en yttre produkt med den så kallade Hodges stjärna-operator.


Enkel räkneregel

Mercedes-stjärnan, minnesregel för beräkning av kryssprodukt.

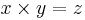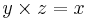För att lätt komma ihåg vilken vektor som bildas vid kryssprodukten av x,y och z kan man tänka enligt följande. Rita upp en plan Mercedes-stjärna enligt bilden. Genom att tänka att tiden på dygnet börjar klockan 00 (12) sätt x längst upp på stjärnan, sedan kommer klockan 4 och näst i alfabetet är y och slutligen klockan 8 görs detsamma z. Tiden går medurs vilket ger: x \times y = z eller y \times z = x osv. Går man istället moturs (tiden blir negativ) fås 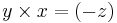y \times x = (-z). 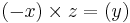Vidare exempel moturs: (-x) \times z = (y).

Kryssprodukten i andra vektorrum

Se även


Nuvola apps edu mathematics-p.svg Denna artikel om algebra är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Kryssprodukt"
Personliga verktyg