Pierre Simon de Laplace
Från Rilpedia
 |
|
| Född: | 23 mars 1749 Beaumont-en-Ange, Normandie, Frankrike |
| Död: | 5 mars 1827 Paris, Frankrike |
| Nationalitet: | Fransk |
| Forskningsområde: | Astronomi Matematik |
| Institutioner: | École Militaire |
| Alma mater: | Caens universitet |
| Akademisk handledare: | Jean le Rond d'Alembert |
| Känd för: | Celest mekanik Laplaceoperatorn Laplacetransform Laplaces ekvation |
Pierre Simon de Laplace, född 23 mars 1749 i Beaumont-en-Ange i Calvados, död 5 mars 1827 i Paris, fransk astronom, matematiker och fysiker. Han har givit sitt namn till Laplaceoperatorn, Laplacetransformen, Laplaces ekvation och Laplaces demon. En av hans elever var Napoleon.
Innehåll |
Karriär
Laplace visade redan tidigt ovanliga anlag för vetenskapen. I synnerhet utövade matematiken dragningskraft på honom, och vid unga år publicerade han en matematisk avhandling i Lagranges Miscellanea taurinensia (1766-69). Denna och några följande avhandlingar fäste uppmärksamheten på Laplace och gav honom en lärarplats i matematik vid militärskolan i Beaumont, vilken han snart lämnade för att inträda som examinator vid artillerikåren i Paris. Han blev 1773 medlem av franska vetenskapsakademin och sedan en av det 1795 upprättade Institut de Frances första medlemmar. Under franska revolutionens första tid tillhörde han med Lagrange kommissionen för mått och vikt och utnämndes till professor vid École normale. Under första konsulatet var han 1799 (i sex veckor) minister för inrikes ärenden samt blev samma år medlem av och 1803 kansler i senaten. Han utnämndes 1804 till greve av Napoleon. 1806 invaldes han som utländsk ledmaot nummer 184 av Kungliga Vetenskapsakademien. 1814 röstade han för bourbonernas restauration samt blev av Ludvig XVIII utnämnd till pär och (1817) markis.
Mécanique céleste
Genom sitt förnämsta arbete, Mécanique céleste (1799), fick Laplace namn som den störste astronomen efter Newton. Han gav i detta arbete en fullständig teori för planetsystemet, uppbyggd på Newtons hypotes om den allmänna gravitationen. Med användning av d'Alemberts, Eulers, Lagranges samt sina egna epokgörande upptäckter i matematik och mekanik lämnade han en inte bara i metodiskt avseende synnerligen elegant framställning av alla de problem, som redan Newton själv behandlat, till exempel tvåkropparsproblemet, precessions- och nutationsfenomenet, fenomenet med ebb och flod, utan även löst det problem, inför vilket Newton med sin tids matematiska hjälpmedel stod kraftlös, det så kallade störningsproblemet. Enligt Laplaces undersökningar kunde planeternas medelavstånd från solen inte undergå annat än små periodiska ändringar. I tredje och fjärde banden av Mécanique céleste lämnar han den speciella och i siffror utförda tillämpningen av sin i de två första banden framställda allmänna teori på planeterna, månen, de övriga satelliterna och kometerna. Liksom hans allmänna teori innehåller huvuddragen av de på planetsystemet gjorda iakttagelserna, så har han i den speciella delen i detalj uppvisat överensstämmelsen mellan teori och observation. Och i varje sådant enskilt fall av överensstämmelse har han gett ett stöd för den hypotes, från vilken han utgått, gravitationshypotesen. Femte bandet innehåller en kort historia över himmelens mekanik samt tillägg till de föregående banden. En allmänfattlig framställning av Mécanique céleste har Laplace själv gett i Exposition du système du monde (1796), där man finner hans nebularhypotes.
Integraler
Det första skedet av sin författarverksamhet ägnade Laplace åt teorin för differential- och differensekvationers integration. Så gav han till exempel en metod att integrera lineära partiella differentialekvationer av 2:a ordningen, integrerade differentialekvationer medelst definita integraler samt behandlade så kallade blandade differensekvationer och framställde integralerna till vissa differensekvationer under form av kedjebråk.
Sannolikhetskalkyl
Från en något senare period kommer upptäckten av de så kallade Laplaces koefficienter (varur teorin för de sfäriska funktionerna sedan utvecklades) och potentialfunktionen, två slag av funktioner som spelar en särdeles viktig roll inom den använda matematiken. Laplaces mest betydande arbete inom den rena matematiken är dock Théorie analytique des probabilités (1812). Första delen av detta arbete upptas av teorin för genererande funktioner. Den andra delen innehåller den egentliga sannolikhetskalkylen och dennas tillämpningar på en mängd vetenskapliga, sociala och praktiska frågor. Där påträffar man även den första framställningen av den för observationers bearbetande så viktiga minsta kvadratmetoden.
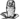 Denna artikel är helt eller delvis baserad på material från Nordisk familjebok, 1904–1926 (Not).
Denna artikel är helt eller delvis baserad på material från Nordisk familjebok, 1904–1926 (Not).



