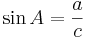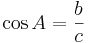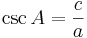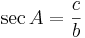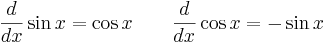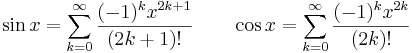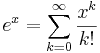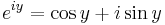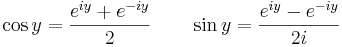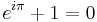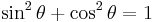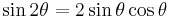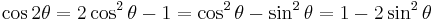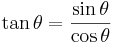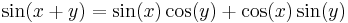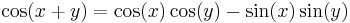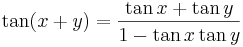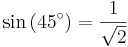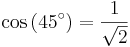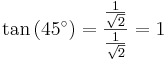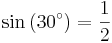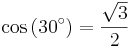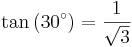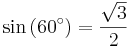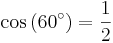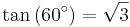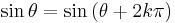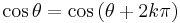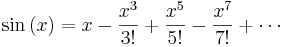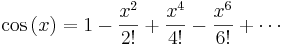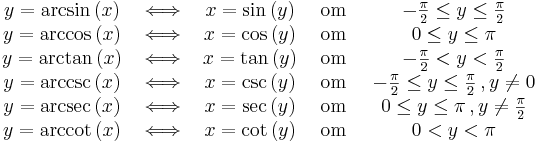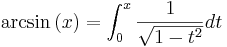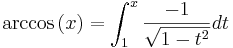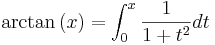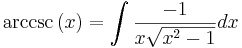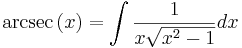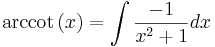Trigonometrisk funktion
Från Rilpedia
Inom tillämpad matematik är trigonometriska funktioner en klass av funktioner vars funktionsvärde beror av en vinkel. Mera specifikt beskriver de hur vinklar och sidor hos trianglar är relaterade till varandra. De har sitt ursprung inom geometri men används inom flera grenar av matematiken liksom inom många tillämpade vetenskaper. De trigonometiska funktionerna är periodiska och är viktiga inom matematisk analys för att studera såväl periodiska som icke-periodiska funktioner (se Fourieranalys).
De trigonometriska funktionerna är
Funktionerna kan definieras på flera olika, men ekvivalenta sätt, exempelvis:
- för allmänna trianglar som kvoten mellan två sidor i en rätvinklig triangel (dock endast för argument i första kvadranten)
- som koordinaterna för en punkt på enhetscirkeln eller kvoter mellan dessa värden
- som en potensserieutveckling
Användbara samband mellan funktionerna finns listade i artikeln Lista över trigonometriska identiteter.
Innehåll |
Geometrisk definition
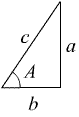
Utgå från en rätvinklig triangel som innehåller vinkeln A:
Hypotenusan är motstående sida till den räta vinkeln, i detta fall c
1). sinus för en vinkel är kvoten av motstående katet och hypotenusan
2). cosinus för vinkeln A är kvoten av närliggande katet och hypotenusan
3). tangens för vinkeln A är kvoten av motstående och närliggande katet
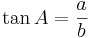 .
.
I främst engelskspråkig litteratur kan man även stöta på ytterligare tre trigonometriska funktioner:
4). cosekant är inverterade värdet av sin A, d.v.s. kvoten av hypotenusan och motstående katet
5). sekant, är inverterade värdet av cos A, d.v.s. kvoten av hypotenusan och närliggande katet
6). cotangens är inverterade värdet av tan A, d.v.s. kvoten av närliggande och motstående katet
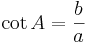 .
.
Alla sex trigonometriska funktionerna baseras alltså på förhållandet mellan två av triangelns tre sidor. Eftersom Pythagoras sats ger oss den tredje sidan om vi känner två, skulle vi strängt taget klara oss med en enda trigonometrisk funktion, exempelvis sin A, och kunna glömma de andra fem. I praktiken används både sinus och cosinus flitigt, och tangens är också ganska vanlig. Med dessa tre kan man utan omvägar ställa upp uttryck för godtyckliga trigonometriska problem. De sista tre funktionerna som utgör rena inverterade värden tillför inte mycket och används därför sällan. Det kan dock vara bra att känna till deras definition.
Analys
Sinus- och cosinusfunktionernas derivator är:
Därmed är Taylorserierna för respektive funktioner
där x anges i radianer.
Vidare har vi att
Om vi sätter x = iy, där i är komplexa enheten, dvs. i2 = -1, kan Eulers formel erhållas:
eller att
Med y = π så fås vad som har kallats The most remarkable formula in the world (Richard Feynman), nämligen Eulers identitet,
Trigonometriska identiteter
- Huvudsida: Lista över trigonometriska identiteter
- Samband för en vinkel
- Samband för 2 vinklar
Se artikeln om derivator för de trigonometriska funktionernas derivator.
Exakta trigonometriska funktionsvärden
För vissa vinklar kan funktionsvärderna beräknas exakt.
Antag en likbent rätvinklig triangel. Den har två lika vinklar θ = 45° = π/4 rad. Vi kan välja a = b = 1. Från detta kan sin, cos och tan för vinkeln 45° beräknas då Pythagoras sats ger hypotenusan c = √(a2 + b2) = √2
Därför,
För att bestämma de trigonometriska funktionernas värden för 60° = π/3 och 30° = π/6 antar vi en liksidig triangel med sidlängden 1 och vinklarna θ = 60°. Genom att bilda höjden mot en av sidorna får vi två nya trianglar med sidorna a = (√3)/2 (höjden), b = 1/2 (halva sidan)och c = 1.
Detta ger
och
Vinklar som kan uttryckas i baser av dessa vinklar (30°, 45°, 60° och 90°) kan sedan beräknas genom att använda trigonometriska identiteter. Exempelvis, cos 22,5° kan beräknas från cos 45° = 1/√2
- 1/√2 = cos(45°) = cos(22,5° + 22,5°) = ... = 2·cos2(22,5°) - 1<=> cos(22,5°) = √(1+1/√2).
Funktionsvärden för godtyckliga vinklar
De trigonometriska funktionerna kan även åskådliggöras med hjälp av enhetscirkeln, cirkeln med radien 1. Enhetscirkeln ger inga nya verktyg för att beräkna funktionsvärderna för olika vinklar, men den innebär ett åskådligt sätt att tolka vinklar utanför intervallet 0°-90° eller 0 rad - π/2 rad
Ekvationen för enhetscirkeln är
- x2 + y2 = 1
och kan grafiskt representeras som
I bilden är ett antal vinklar utritade, uttryckta i radianer (läs artikeln om grader). Vinklar mäts som positiva i moturs riktning och som negativa i medurs riktning. Linjen som skär enhetscirkeln bildar en vinkel θ med positiva x-axeln där skärningspunkten har koordinaterna cosθ och sinθ. Triangeln i figuren visar att radien är lika med hypotenusan och har längden 1, sinθ = y/1 och cosθ = x/1. Vinklar större än 2π eller mindre än -2π motsvarar rotationer större än ett varv, vilket illustrerar att sinus- och cosinusfunktionerna är periodiska (se periodiska funktioner) med perioden 2π.
Sambandet
gäller för alla vinklar θ och heltal k.
Sinus- och cosinusfunktionerna är periodiska: 
Serieutveckling
Om vinklarna anges i radianer kan man skriva (se maclaurinutveckling)
Med hjälp av serieutveckling kan trigonometriska funktioner definieras även för komplexa värden.
Inversa funktioner
Inverser till de trigonometriska funktionerna existerar endast på begränsade intervall. Det finns funktioner dock som är definierade på olika interval som ibland oegentligt betecknas som inverser. Dessa kallas egentligen arcus-funktioner (till exempels arcus cosinus) I allmänhet brukar de förkortas med arctan, arcsin och arccos, men på miniräknare och i mindre nogräknade matematiska skrifter brukar dessa funktioner skrivas tan − 1, sin − 1 respektive cos − 1. Funktionerna används till exempel för att beräkna värdet på en okänd vinkel i en rätvinklig triangel där sidlängderna är kända. I en rätvinklig triangel där kateterna har längderna a och b, har vinkeln mellan hypotenusan och kateten a värdet arctan(b/a) och vinkeln mellan hypotenusan och kateten b värdet arctan(a/b).
De inversa funktionerna motsvarar integralerna
Egenskaper och tillämpningar
Trigonometriska funktioner är, som benämningen antyder, av betydelse inom trigonometri, bland annat genom följande satser:
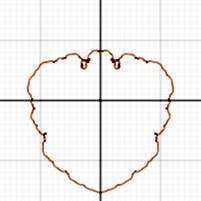
{x, y} = Σ_n=1→∞
(1/F(n+1)){sin(θF(n)),cos(θF(n))}
Se även
Externa länkar
- GonioLab: Visualisering av enhetscirkeln, trigonometriska och hyperboliska funktioner (Java Web Start)