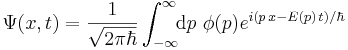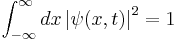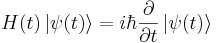Schrödingerekvationen
Från Rilpedia
| Kvantmekanik |
|---|
|
Teori:
Persongalleri |
I fysiken beskriver schrödingerekvationen, föreslagen av den österrikiske fysikern Erwin Schrödinger år 1925, rums- och tidsberoendet för kvantmekaniska system. Den är av central betydelse för icke-relativistisk kvantmekanik, där den spelar en roll analog med Newtons andra lag i klassisk mekanik. Schrödingerekvationen är empiriskt belagd. Ett fenomen är kvantiserat om dess lösning av Schrödinger-ekvation innehåller ett uppräkneligt antal energinivåer, s.k. kvantnivåer.
(För det relativistiska fallet, se Klein-Gordon-ekvationen och Diracekvationen.) Schrödinger grundlade sitt arbete på de Broglies ekvation som gav den korresponderande våglängden för en materiapartikel. Schrödinger misslyckades dock med att forma sin ekvation relativistiskt, och därför har ekvationen endast begränsad tillämpbarhet, till exempel på väteatomen.
I en rumsdimension är den tidsberoende schrödingerekvationen
där Ψ är sannolikhetsamplituden (vågfunktionen) och V är den potentiella energin. Den tredimensionella motsvarigheten är
där man brukar införa hamiltonoperatorn 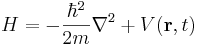 .
.
Innehåll |
Intuitiv tolkning av ekvationen
Vågfunktionen (Ψ) för ett kvantmekaniskt system ger oss information om hur vi kan beräkna sannolikheter att systemet skall befinna sig i olika tillstånd; för en enskild partikel kan 'tillståndet' i fråga vara att den skall röra sig inom en cirkel, vars centrum är i origo och vars radie är en centimeter, under 10 minuter. Sannolikheterna förändras allteftersom tiden går och de är också beroende på var någonstans partikeln befinner sig; matematiskt innebär detta att vågfunktionen är en funktion som beror av tiden (t) och positionen i rummet (x):
Schrödingers ekvation talar om hur vågfunktionen förändras då tiden går, vilket beskrivs matematiskt med den partiella derivatan av vågfunktionen med avseende på tidsvariabeln:
Schrödinger säger att förändringen beror på hur snabbt partikeln rör sig och vilka hinder den upplever under sin rörelse:
Ett annat sätt att uppfatta Schrödingerekvationen är som en beskrivning av rörelsen hos en partikel som skuttar runt slumpmässigt (diffunderar) och som stöter på hinder i sin rörelse:
Notera att själva rörelsen hos partikeln inte beskrivs av Schrödingerekvationen – för en sådan beskrivning behöver man en så kallad stokastisk differentialekvation – utan Schrödingerekvationen bara ger oss information om sannolikheter att partikeln skall vara på vissa platser under vissa tider.
Sannolikheten att partikeln under tio minuter skall röra sig inom cirkeln D, vars centrum är origo och vars radie är en centimeter, ges av följande integral av vågfunktionen:
Om vi har funnit lösningen till Schrödingerekvationen så vet vi hur vågfunktionen ser ut och då kan vi beräkna denna dubbelintegral.
Exempel
Plan våg
En plan våg kan beskrivas endimensionellt. För en fri partikel (V = 0) är den generella lösningen
där φ är ett vågpaket, dvs en fördelning av rörelsemängder, p, och E(p) = p2 / 2m är energin hos en partikel med rörelsemängd p.
Partikel i låda
"Lådan" består av en potential som är oändlig utanför och konstant in i lådan. Lösningarna är vågor för fria partiklar som uppfyller randvillkoren att vågfunktionen måste vara noll utanför lådan. Detta leder till stående vågor med ett diskret energispektrum.
Speciella relativitetsteorin
Att denna ekvation inte är kompatibel med speciella relativitetsteorin inses då differentialekvationen är av första ordningen i tiden, men av andra ordningen i variabeln x. Vidare kan sägas att ψ(x,t) är en komplexvärd funktion (se komplexa tal) och att 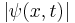 är stor där partikeln förväntas vara. Max Born postulerade att funktionen
är stor där partikeln förväntas vara. Max Born postulerade att funktionen 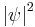 motsvarar sannolikheten för att en partikel befinner sig i rumsintervallen x + dx och inom tidsintervallen t + dt. Detta medför att vi kan förstå normaliseringsfaktorn i lösningen ovan, då följande villkor ställs på lösningarna, eftersom en partikel med nödvändighet måste befinna sig någonstans i rummet.
motsvarar sannolikheten för att en partikel befinner sig i rumsintervallen x + dx och inom tidsintervallen t + dt. Detta medför att vi kan förstå normaliseringsfaktorn i lösningen ovan, då följande villkor ställs på lösningarna, eftersom en partikel med nödvändighet måste befinna sig någonstans i rummet.
Funktionalanalys
I kvantmekanik är varje system associerat med ett komplext hilbertrum sådant att de möjliga tillstånden i systemet är beskrivet av en linjärkombination av enhetsvektorer i en sådan rymd. Respektive tillståndsvektor kodifierar sannolikheterna för utfallen av alla möjliga mätningar applicerade på system. Eftersom systemets tillstånd generellt förändras över tiden, är tillståndsvektorn en funktion över tiden. Schrödingerekvationen ger en kvantitativ beskrivning av förändringen av tillståndsvektorn.
Med användning av Diracs notation kan vi skriva tillståndsvektorn vid tid t som |ψ(t)〉.
Schrödingerekvationen är då:
Se även
- Värmeledningsekvationen
- Hartree-Fock - En approximativ metod för beräkningar på flerelektronsystem, som bygger på Schrödingerekvationen.
- Hamilton-Jacobi ekvationen
- Poissonparentes
- Kvantmekanik




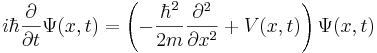
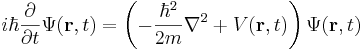
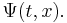
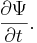
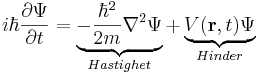

![\int_{t \in [0,10]} \int_{x \in D} \vert \Psi(t,x) \vert ^2 \, dt dx.](/w/images/sv.rilpedia.org/math/9/5/6/956565e4f7848c4820995521326140ec.png)