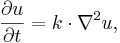Värmeledningsekvationen

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Värmeledningsekvationen, diffusionsekvationen, en partiell differentialekvation med ett antal tillämpningar i fysiken.

Värmeledningsekvationen kan skrivas:

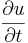\frac{\partial u}{\partial t} = k \cdot \nabla^2 u,

där \frac{\partial u}{\partial t} betecknar förändringshastigheten hos funktionen u(t,x) med avseende på tiden, och 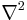\nabla^2 betecknar laplaceoperatorn.

Värmeledningsekvationen kan användas för att beskriva värmespridning i ett medium. Funktionen u(t,x) betecknar då temperaturen i mediet och k är en konstant som beror av materialets värmeledningsförmåga, densitet och värmekapacitet.

Se även


Lebesgue Icon.svg Denna artikel om matematisk analys är bara påbörjad. Du kan hjälpa till genom att utöka den.
Stylised Lithium Atom.svg Denna artikel om fysik är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/V%C3%A4rmeledningsekvationen"
Personliga verktyg