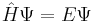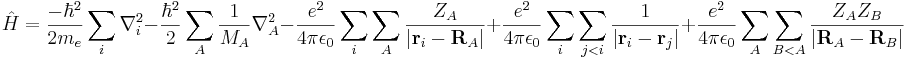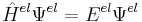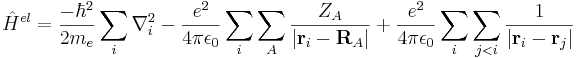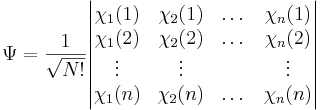Hartree-Fock

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Hartree-Fock molekylorbitalteori (Hartree-Fock-metoden) är inom beräkningsfysik och beräkningskemi en approximativ metod för att bestämma energin hos grundtillståndsvågfunktionen och grundtillståndsenergin hos ett kvantmekaniskt flerkroppssystem, som kan vara till exempel en molekyl eller ett fast ämne ("det fasta tillståndet").

Innehåll

Beskrivning av teorin

Schrödingerekvationen som grund

Hartree-Fockteorin bygger vidare på den berömda Schrödingerekvationen. Schrödingerekvationen är anmärkningsvärd genom att den så lätt kan formuleras för system med i princip hur många kärnor och elektroner som helst. Om Schrödingerekvationen tillämpades strikt på ett sådant system skulle den dessutom ge mycket goda och verklighetsnära resultat.

Den generella Schrödingerekvationen för ett system med flera kärnor och flera elektroner kan skrivas:

{\hat{H}\Psi = E\Psi}

E är här den totala energin i systemet, ψ är en vågfunktion för n stycken elektroner, som är beroende både av kärnornas positionen och identitet (hur stora atomkärnorna är), samt det totala antalet elektroner. Hamiltonoperatorn, 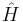\hat{H}, ger ett "recept" på hur de kinetiska och potentiella energierna för var och en av partiklarna ska specificeras, och kan skrivas:


\hat{H} = {- \hbar^{2} \over {2 m_e}} \sum_i\nabla^{2}_{i} - {\hbar^2 \over 2}\sum_A {1 \over M_A} \nabla^{2}_{A} - {e^2 \over {4\pi\epsilon_0}}\sum_i\sum_A \frac{Z_A}{|\mathbf{r}_i-\mathbf{R}_A|} + {e^2 \over {4\pi\epsilon_0}}\sum_{i}\sum_{j<i} \frac{1}{|\mathbf{r}_i-\mathbf{r}_j|} + {e^2 \over {4\pi\epsilon_0}}\sum_{A}\sum_{B<A} \frac{Z_A Z_B}{|\mathbf{R}_A-\mathbf{R}_B|}

där i och j används som summationsindex för elektroner och A och B för atomkärnorna.

Hamiltonoperatorn är alltså ett polynom av summor. Termerna anger följande storheter (i beskriven ordning):

  1. Kinetisk energi hos elektronerna
  2. Kinetisk energi hos kärnorna
  3. Potentiell energi beroende på skillnad i elektrisk laddning mellan elektroner och kärnor
  4. Potentiell energi beroende på skillnad i elektrisk laddning mellan elektroner inbördes
  5. Potentiell energi beroende på skillnad i elektrisk laddning mellan kärnor inbördes

Approximationer i Hartree-Fockmetoden

Schrödingerekvationen har tyvärr visat sig omöjlig att lösa i praktiken, förutom för system med en enda elektron, d.v.s. väteatomen. För att praktiskt kunna genomföra beräkningar med kvantmekanik som teoretisk grund på större system än så är det därför nödvändigt att göra följande tre approximationer, som utgör grunden för alla Hartree-Fockmodeller:

Born-Oppenheimerapproximationen

Atomkärnor rör sig mycket långsammare än elektroner och kan därför betraktas som stillastående/stationära. Detta kallas Born-Oppenheimerapproximationen. Approximationen ger den s.k. elektroniska Schrödingerekvationen. Denna kan skrivas:

\hat{H}^{el}\Psi^{el} = E^{el}\Psi^{el}

Hamiltonoperatorn för den elektroniska Schrödingerekvationen kan skrivas:


\hat{H}^{el}= \frac{- \hbar^2}{2 m_e} \sum_i \nabla^{2}_{i} - \frac{e^2}{4\pi\epsilon_0} \sum_i\sum_A \frac{Z_A}{|\mathbf{r}_i-\mathbf{R}_A|} + \frac{e^2}{4\pi\epsilon_0} \sum_i\sum_{j<i} \frac{1 }{|\mathbf{r}_i-\mathbf{r}_j|}


Här är alla termerna för kinetisk energi (rörelseenergi) för kärnorna samt för potentiell energi mellan kärnorna utelämnade jämfört med ekvationen för hamiltonoperatorn i den vanliga Schrödingerekvationen. Kvar har vi endast:

  1. Kinetisk energi hos elektronerna
  2. Potentiell energi beroende på skillnad i elektrisk laddning mellan elektroner och kärnor
  3. Potentiell energi beroende på skillnad i elektrisk laddning mellan elektroner och elektroner

För att erhålla ett korrekt värde på den totala energin för systemet måste dessutom resultatet från den elektroniska Schrödingerekvationen kompletteras med en konstant för kärn-kärn-laddningsenergin.

Hartree-Fockapproximationen

Hartree-Fockapproximationen innebär att man antar att elektronerna rör sig helt oberoende av varandra. Med denna approximation kan systemet beskrivas med endaste en elektronorbital per elektron, vilket minskar komplexiteten på beräkningarna enormt.

För att den resulterande funktionen dessutom ska bete sig antisymmetriskt vid byte av två elektronkoordinater (vilket är en inneboende egenskap hos kvantmekaniska system) så skrivs systemet som en slaterdeterminant, där varje rad i determinantmatrisen motsvarar en elektron. Determinantmatriser har nämligen den inneboende egenskapen att om man byter plats på två rader så erhålls samma värde som tidigare men med bytt tecken.


{\Psi} = {1 \over \sqrt{N!}} \begin{vmatrix} \chi_1(1)&\chi_2(1)&\dots&\chi_n(1)\\ \chi_1(2)&\chi_2(2)&\dots&\chi_n(2)\\ \vdots&\vdots&&\vdots\\ \chi_1(n)&\chi_2(n)&\dots&\chi_n(n)\\ \end{vmatrix}

LCAO-approximationen

LCAO-approximationen innebär att man betraktar molekylorbitalerna som linjärkombinationer av atomorbitaler, vilket gett LCAO dess namn: "Linear Combination of Atomic Orbitals". Orsaken till att man vill linjärkombinera atomorbitaler är att man därigenom med relativt få "byggstenar" kan generera en relativt verklighetstrogen approximation till den verkliga molekylorbitalen.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Hartree-Fock"
Personliga verktyg