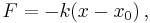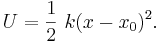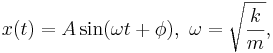Harmonisk oscillator

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

En harmonisk oscillator är inom fysiken ett system där den återdrivande kraften F är proportionell mot avvikelsen från jämviktsläget x0 , det vill säga system som kan beskrivas med Hookes lag:

F = -k (x-x_0) \, ,

där k är systemets kraftkonstant. Integration ger systemets energi U som en harmonisk, det vill säga kvadratisk potential:

U = \frac12 \ k (x - x_0)^2.

Klassisk mekanik

Genom att använda F = ma = m d²x/dt² får man en differentialekvation med den allmänna lösningen

x(t) = A \sin(\omega t + \phi),\ \omega = \sqrt\frac{k}{m},

där A och φ är integrationskonstanter. Oscillationsfrekvensen f = 2πω är alltså större för högre kraftkonstant och mindre massa.

Ofta används harmoniska oscillatorn för att idealiserat beskriva approximationer till system som periodiskt växlar läge kring en jämviktspunkt (till exempel en pendel). Det visar sig att många system uppvisar denna egenskap i en första approximation, till exempel atomer i en kristallstruktur.

Kvantmekanik

Den harmoniska oscillatorns energinivåer och täthetsfunktioner enligt Schrödingerekvationen

För vibrationer av atomer är det dock ofta nödvändigt att tillämpa kvantmekanik. Schrödingerekvationen för en partikel i en harmonisk potential kan lösas exakt.


Stylised Lithium Atom.svg Denna artikel om fysik är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Harmonisk_oscillator"
Personliga verktyg