Partikel i låda
Från Rilpedia


Partikel i låda är en förhållandevis enkel kvantmekanisk modell som används för att illustrera grundläggande kvantmekaniska egenskaper. Den kan beskrivas i godtyckligt antal dimensioner, men det enklaste fallet är en dimension. I en dimension består modellen av en partikel som rör sig längs x-axeln. Mellan x=0 och x=L är potentialen V(x)=0, medan den är oändlig utanför denna "låda". Där potentialen är oändlig är sannolikheten för att finna partikeln 0, så partikeln måste befinna sig mellan x=0 och x=L.
Innehåll |
Klassisk beteende
Klassiskt studsar partikeln fram och tillbaka mellan dessa två vändpunkter, med hastighet +v och -v. Sannolikheten att påträffa partikeln är oberoende av positionenen mellan väggarna. Klassiskt kan partikelns kinetiska energi ha vilket värde som helst, även noll.
Kvantmekaniska vågfunktioner
Men när lådan är smal är de klassiska lagarna inte längre en bra approximation. Om man vet partikelns läge med en osäkerhet Δx, säger Heisenbergs obestämbarhetsrelation att partikeln måste ha rörelsemängd p och -p större än noll.
Mellan väggarna blir den tidsoberoende Schrödingerekvationen
där
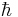 är Plancks reducerade konstant
är Plancks reducerade konstant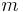 är partikelns massa
är partikelns massa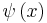 är den komplexvärda stationära tidsoberoende vågfunktionen som beskriver partikeln, och som vi vill hitta
är den komplexvärda stationära tidsoberoende vågfunktionen som beskriver partikeln, och som vi vill hitta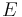 är systemets energi, som är ett reellt tal.
är systemets energi, som är ett reellt tal.
När man löser denna differentialekvation och utnyttjar de randvillkor som ges av potentialen och att partikeln måste befinna sig någonstans får man ut vågfunktionerna och energierna
där n är ett positivt heltal. Trots att modellen är så enkel har den grundläggande kvantmekaniska egenskaper som åtskilda (diskreta) energinivåer (eftersom n måste vara heltal kan inte E vara vilket tal som helst) och en nollpunktsenergi som inte är 0 (n får inte vara mindre än 1, och n=1 ger E>0).
Stationära tillstånd
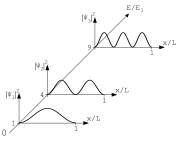
Vågfunktionen har sedan Max Born tolkats som att |ψ(x)|² ger sannolikheten att hitta partikeln nära x. För den tidsoberoende Schrödingerekvationens egentillstånd är dessa täthetsfunktioner konstanta i tid, eftersom den tidsberoende Schrödingerekvationen bara ger en fasfaktor 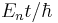 . Dessa stationära tillstånd har för n > 1 noder där vågfunktionen är 0 inuti lådan, vilket innebär att sannolikheten för att partikeln befinner sig just där är 0, trots att den kan befinna sig på båda sidor om noden.
. Dessa stationära tillstånd har för n > 1 noder där vågfunktionen är 0 inuti lådan, vilket innebär att sannolikheten för att partikeln befinner sig just där är 0, trots att den kan befinna sig på båda sidor om noden.
Icke-stationära tillstånd
Linjära kombinationer av egentillstånden är också lösningar av Schrödingerekvationen. Men eftersom komponenterna har olika egenenergier, roterar deras faser med olika hastighet så att summan inte har konstant amplitud. Täthetsfördelningen är därför inte konstant i tid.
Om vågfunktionen är en summa äv två egentillstånd med energier Em och En, oscillerar täthetsfunktionen med en frekvens Em-En/h. Om partikeln har en elektrisk laddning, avger den elektromagnetisk strålning med denna frekvens, som har en fotonenergi motsvarande energiskillnaden mellan tillstånden.
Källor
- Artikeln är, helt eller delvis, en översättning från engelskspråkiga Wikipedia.
- Griffiths, David J.: Introduction to Quantum Mechanics, Prentice Hall, Upper Saddle River 2005 "2.2",, andra upplagan. ISBN 0-13-191175-9.




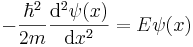
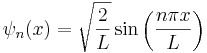
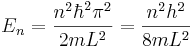
.gif/180px-Particle_in_a_box_(time_evolution).gif)