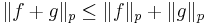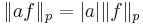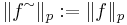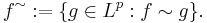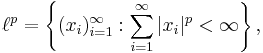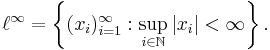Lp-rum
Från Rilpedia
Ett Lp-rum är ett funktionsrum inom matematik. Lp-rummet består av funktioner som är p-integrebara. Man behöver Lp-rummet till exempel inom måtteori och funktionalanalys.
Innehåll |
Formell definition
Lp-rummet är en måtteoretisk konstruktion och man kan bara definiera det för måttrum.
Låt 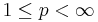 och
och 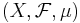 vara ett måttrum så att måttet µ är ett fullständigt mått. Man behöver fullständighet här eftersom man vill integrera alla delmängder för en nollmängd.
vara ett måttrum så att måttet µ är ett fullständigt mått. Man behöver fullständighet här eftersom man vill integrera alla delmängder för en nollmängd.
För mätbara funktioner 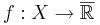 definierar man Lp-normen
definierar man Lp-normen
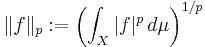 ,
,
dvs Lp-normen är en p-rot av måttintegralen för funktionen | f | p. För 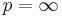 definieras
definieras 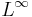 -normen:
-normen:
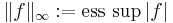 ,
,
där ess sup är väsentligt supremum.
Lp-normen, med 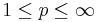 , är inte en norm för alla mätbara funktioner. Men man kan definiera ett rum, som kallas Lp-rummet, där det är en norm. Lp-rummet, för ett fixt p, är mängden:
, är inte en norm för alla mätbara funktioner. Men man kan definiera ett rum, som kallas Lp-rummet, där det är en norm. Lp-rummet, för ett fixt p, är mängden:
 .
.
Lp-rummet är ett vektorrum. Tyvärr, eftersom man har definierat Lp-rummet med en måttstruktur så är Lp-normen bara en seminorm, dvs
och
för 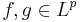 och
och 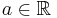 men det finns måttrum och funktioner där
men det finns måttrum och funktioner där
 men
men 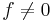
exempelvis 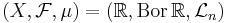 och
och  .
.
Å andra sidan kan man definiera en ekvivalensrelation i Lp genom att
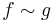 om och endast om
om och endast om 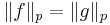
och definiera Lp-normen för ekvivalensklasser
där f˜ är ekvivalensklassen med representant f:
Med denna struktur fås att 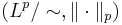 är ett normerat rum. Man menar ofta
är ett normerat rum. Man menar ofta 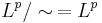 .
.
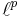 -rum
-rum
Som ett specialfall av Lp-rum kan man få de så kallade 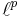 -rummen. Om X är uppräknelig och måttet µ är räknemåttet betecknas
-rummen. Om X är uppräknelig och måttet µ är räknemåttet betecknas
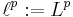 ,
,
så att för 
dvs, 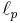 kan ses som alla följder i X så att summan av termerna upphöjt till p konvergerar.
kan ses som alla följder i X så att summan av termerna upphöjt till p konvergerar.
Man får också:
dvs, 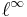 -rummet är rummet av alla begränsade följder.
-rummet är rummet av alla begränsade följder.
Egenskaper
Nedan finns några egenskaper för Lp-rummen och normerna.
Olikheter
Hölders olikhet: om 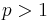 och
och 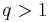 med
med
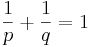 ,
,
och 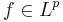 och
och 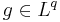 så är
så är
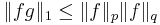 .
.
Om 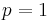 och
och 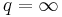 så är
så är
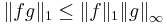 .
.
Talen p och q kallas för Hölderkonjugat.
Minkowskis olikhet: Man kallar ofta triangelolikheten
när 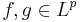 för Minkowskis olikhet.
för Minkowskis olikhet.
Dualrummet
Om p och q är Hölderkonjugat så är 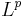 :s dualrummet
:s dualrummet 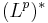 isomorf till
isomorf till 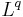 , dvs
, dvs
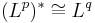 .
.
Därför säger man ofta att Lp:s dualrum är Lq.
Notera att det finns måttrum där 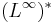 inte är isomorf med
inte är isomorf med 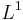 .
.
Se även
Referenser
- W. Rudin, Functional analysis, McGraw-Hill, 1991
- P. Halmos, Measure theory, D. van Nostrand and Co., 1950
- M. E. Munroe, Introduction to Measure and Integration, Addison Wesley, 1953
- R. M. Dudley, Real Analysis and Probability, Cambridge University Press, 2002
- G. B. Folland, Real Analysis: Modern Techniques and Their Applications, John Wiley, 1984