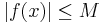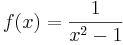Begränsad funktion
Från Rilpedia
En begränsad funktion är inom matematik en reell eller komplex funktion f, definierad på någon mängd X, sådan att mängden av funktionsvärdena av f är begränsad mängd. Med andra ord existerar det något tal M så att:
för alla x i X.
Man säger även att en funktion f är uppåt begränsad om det finns ett A så att 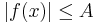 för alla x i X och att f är nedåt begränsad om det finns ett B så att
för alla x i X och att f är nedåt begränsad om det finns ett B så att 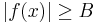 för alla x i X.
för alla x i X.
Ett specialfall fås då X är de naturliga talen, då funktionen blir en talföljd (an) som sägs vara begränsad om det existerar något tal M så att 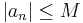 för alla naturliga tal n.
för alla naturliga tal n.
En generalisering av begreppet fås i metriska rum, då en funktion definierad på någon mängd X och tar värden i något metriskt rum Y är begränsad om det i Y existerar ett element a så att det existerar ett tal M så 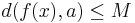 för alla x i X.
för alla x i X.
Exempel
- Funktionen sinus för de reella talen (dock inte för de komplexa) tar endast värden mellan -1 och 1 och är alltså nedåt begränsad av -1 och uppåt begränsad av 1.
- Funktionen
definierad för alla reella x som inte är -1 eller 1 är inte begränsad, då funktionen växer obegränsat då x går mot 1 eller -1. Om definitionsmängden tas att vara exempelvis intervallet 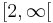 är den dock begränsad.
är den dock begränsad.
- Varje kontinuerlig funktion från ett kompakt rum till ett metriskt rum är begränsad.
- Dirichlets funktion är begränsad.