Triangelolikheten
Från Rilpedia
Triangelolikheten är en matematisk olikhet som säger att i en triangel är längden av en viss sida mindre än summan av längderna av de två övriga sidorna, men större än differensen dem emellan.
Den är giltig i en stor uppsätting rum, bland annat för de reella talen.
Innehåll |
Normerat vektorrum
I ett normerat vektorrum V uttrycks triangelolikheten
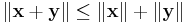 för alla
för alla 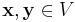 . Likhet gäller om och endast om
. Likhet gäller om och endast om 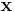 och
och 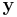 är parallella.
är parallella.
Reella tallinjen
Den reella tallinjen är ett normerat vektorrum, med absolutbeloppet som norm. Triangelolikheten för de reella talen skrivs därmed
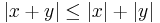 Här gäller likhet om x och y har samma tecken.
Här gäller likhet om x och y har samma tecken.
Komplexa talplanet
Inom komplex analys ser olikheten ut som följer:
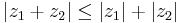 Här gäller likhet om arg(z1) = arg(z2)
Här gäller likhet om arg(z1) = arg(z2)
Samtidigt gäller (se följdsatsen nedan) att ett tals absolutbelopp är större än differensen av komponenterna (eller lika med, om arg(z1) = − arg(z2)):
Metriska rum
Triangelolikheten ingår som ett av de definierande axiomen för metriken d i ett metriskt rum 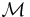 .
.
Den säger att summan av avståndet mellan två punkter p och q alltid är mindre eller lika med summan av avstånden mellan punkt p och en godtycklig punkt r, samt avståndet från r till q, dvs:
där d(p,q) betecknar avståndet mellan p och q. Funktionen 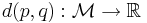 kallas metriken, eller avståndsfunktionen. Notera att det är avståndet mellan två objekt som definierar rummet, inte tvärt om.
kallas metriken, eller avståndsfunktionen. Notera att det är avståndet mellan två objekt som definierar rummet, inte tvärt om.
Följdsats
Ur triangelolikheten följer att
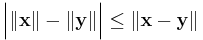 och | d(p, r) - d(r, q) | ≤ d(p, q)
och | d(p, r) - d(r, q) | ≤ d(p, q)
vilket betyder att normen 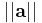 och avståndsmåttet d(a,b) är Lipschitz-kontinuerliga och därmed även kontinuerliga.
och avståndsmåttet d(a,b) är Lipschitz-kontinuerliga och därmed även kontinuerliga.
Serier och integraler
Den vanliga triangelolikheten har några följder:
Med induktion man kan visa att:
för 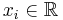 och
och 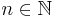 . För absolutkonvergenta serier, dvs:
. För absolutkonvergenta serier, dvs:
finns en triangelolikhet:
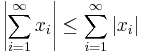 .
.
Dessutom, för en integral, exempelvis Riemannintegralen, kan man med definitionen av supremum och infimum visa att det finns en triangelolikhet:
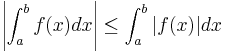 ,
,
om 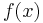 är Riemannintegrerbar.
är Riemannintegrerbar.




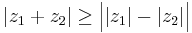
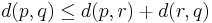
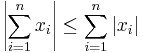
![\sum_{i=1}^\infty |x_i| \in [0,\infty]](/w/images/sv.rilpedia.org/math/b/1/2/b1294f48d12b3279a2b11f0104e56985.png)