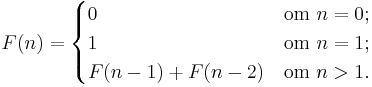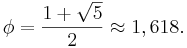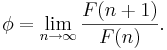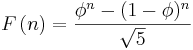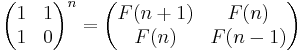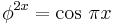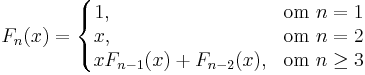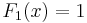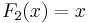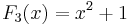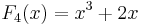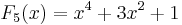Fibonaccital

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Tessellation med kvadrater som har fibonaccital som sidlängd.

Ett fibonaccital ingår i en sekvens av heltal, där varje tal är summan av de två föregående; de två första talen är 0 och 1. Matematiskt innebär det att fibonaccitalen är en sekvens F(n), definierad rekursivt enligt:

F(n)= \begin{cases} 0 & \mbox{om }n=0; \\ 1 & \mbox{om }n=1; \\ F(n-1)+F(n-2) & \mbox{om }n>1. \end{cases}

De första Fibonaccitalen är [1]:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025 ..

Innehåll

Bakgrund

Talen är uppkallade efter italienaren Leonardo Pisano Fibonacci som på 1200-talet använde dem för att beskriva tillväxten hos kaniner. Talen beskriver antalet kaninpar i en grupp kaniner efter n månader om man antar att

  • Det finns endast ett par nyfödda kaniner den första månaden.
  • Nyfödda kaniner blir könsmogna från månad två och framåt.
  • Det uppstår inga genetiska problem på grund av inavel.
  • Varje månad föds en unge per könsmogen kanin.
  • Ingen av kaninerna dör.

Fibonaccitalen beskrevs dock redan under 500-talet f.Kr. av den indiske matematikern Pingala.

Anknytning till det gyllene snittet

Fibonaccisekvensen är relaterad till det gyllene snittet, talet

\phi = \frac{1 + \sqrt{5}}{2} \approx 1,618.

Särskilt gäller att kvoten mellan efterföljande fibonaccital konvergerar mot det gyllene snittet:

\phi = \lim_{n\to\infty} \frac{F(n+1)}{F(n)}.

Med hjälp av det gyllene snittet kan man även ange det nte fibonaccitalet på explicit form:

F\left(n\right) = {{\phi^n-(1-\phi)^n} \over {\sqrt 5}}

Den här identiteten är känd som Binets formel efter Jacques Binet.

Talteoretiska egenskaper

Fibonaccitalens delbarhet har studerats flitigt inom talteorin. De kan bland annat visas uppfylla

sgd(F(n),F(m)) = F(sgd(n,m))

där sgd betecknar den största gemensamma delaren. Det följer att F(n) är delbart med F(m) om och endast om n är delbart med m, med triviala undantag för n mindre än 4.

Frågan om huruvida det finns oändligt många primtal i fibonaccisekvensen är ett berömt olöst problem inom matematiken. Med undantag för n = 4 kan F(n) endast vara ett primtal om n också är det, men omvändningen gäller inte: om n är ett primtal behöver inte nödvändigtvis F(n) också vara primt. Följden av prima fibonaccital inleds med 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, 433494437, ... [2].

Det största fibonaccital som bevisats vara primt är det 17103-siffriga F(81839). Ännu större fibonaccital är kända som klarar pseudoprimtalstest, det största F(604711) med 126377 siffror.

Känt är att fibonaccitalens faktoriseringar innehåller oändligt många olika primtal. Robert Daniel Carmichael har visat att varje fibonaccital efter F(12) har minst en primtalsfaktor som inte delar något tidigare tal i sekvensen.

Fibonaccisekvensen är periodisk modulo varje positivt heltal m. Exempelvis är fibonaccitalen modulo 2 lika med sekvensen 1, 1, 0, 1, 1, 0, ..., som har perioden 3. Perioden π(m), döpt till "pisanoperioden", är för m = 1, 2, ... lika med 1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, ... [3].

Eftersom periodiciteten innefattar alla tiopotenser m = 10n upprepas varje siffra och grupp av siffror periodiskt: till exempel upprepas samma avslutande siffra alltid vart π(10) = 60:e fibonaccital, och samma två avslutande siffror återkommer vart π(100) = 300:e fibonaccital. Då n > 3 ges perioden för de n sista siffrorna av den explicita formeln 15 · 10n−1. Ett alternativt perspektiv är att det för varje fibonaccital F(n) finns oändligt många större fibonaccital vars siffror slutar med F(n).

Matrisform

Följande matrisidentitet ger en explicit formel för fibonaccitalen som lämpar sig särskilt väl för att med dator beräkna mycket stora fibonaccital:

\begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^n = \begin{pmatrix} F(n+1) & F(n) \\ F(n) & F(n-1) \end{pmatrix}

Förekomst i naturen

Solros med frön ordnade i 21 spiraler medsols och 34 spiraler motsols ut från centrum framifrån betraktat.

Fibonaccitalen förekommer i spiralstrukturer i naturen, exempelvis i kottar, snäckor och solrosor. Antalet spiraler räknat motsols respektive medsols utgör i sådana strukturer två efterföljande fibonaccital. Så stora fibonaccital som 233 har påträffats.

Generaliseringar

Utökning av index

Genom att lösa ut F(n) som differensen F(n+2) − F(n+1) kan fibonaccisekvensen utökas i negativ riktning till

..., 13, -8, 5, -3, 2, -1, 1, 0, 1, 1, 2, 3, 5, 8...

som uppfyller F(−n) = (−1)n+1 F(n) för alla heltal n. Samma utökning fås genom direkt insättning av negativa index i Binets formel, som även låter fibonaccifunktionen F(x) definieras för reella och komplexa tal x. Den kontinuerliga funktionen F(x) har de oändligt många nollställena x = 0 och x ≈ 0,18380, 1,5708, 2,4704, 3,5109, ... som precis svarar mot lösningarna till ekvationen

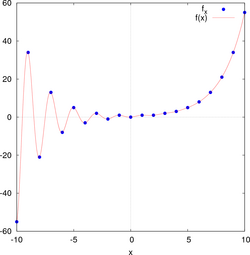
Fibonaccifunktionen F(x) för −4 ≤ x ≤ 4. Fibonaccitalen F(n) är markerade som punkter på kurvan. Värt att notera är att fibonaccitalen approximerar men inte är exakt lika med funktionens extrempunkter.
\phi^{2x} = \cos \, \pi x

och närmar sig n + 1/2 för stora negativa n.

Andra begynnelsevärden

Fibonaccitalen definieras genom differensekvationen

F(n) = F(n − 1) + F(n − 2)

och två begynnelsevärden. Andra val av begynnelsevärden ger upphov till andra sekvenser, exempelvis lucastalen som ges av L(1) = 1, L(2) = 3 och fortsätter med 4, 7, 11, 18, 29, etcetera. Sådana sekvenser uppfyller egenskaper liknande dem hos fibonaccitalen: exempelvis har alla sekvenser på denna form det gyllene snittet som gränsvärde för kvoten mellan intilliggande tal.

De funktioner g som löser fibonaccisekvensens differensekvation har formen

g(n) = aF(n) + bF(n + 1)

för godtyckliga tal a och b, och kallas ibland mer allmänt för fibonaccisekvenser. Fibonaccisekvenserna utgör ett vektorrum med funktionerna n ↦ F(n) och n ↦ F(n + 1) som basvektorer. En följd är att lucastal kan omvandlas till fibonaccital och vice versa genom basbyte. Exempelvis ges det n-te lucastalet av L(n) = 2F(n) + F(n+1).

Fibonaccitalen kan ytterligare generaliseras genom att variera formen på differensekvationen. Exempelvis definieras Pells tal av ekvationen P(n) = 2P(n−1) + P(n-2) med samma begynnelsevärden som för fibonaccisekvensen. Genom att låta varje tal i sekvensen vara summan av fler än två föregående tal fås följande generaliseringar:

Ordning Namn Formel för f(n) Inledande termer
3 tribonaccital f(n−1) + f(n−2) + f(n−3) 0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, ... [4]
4 tetranaccital f(n−1) + f(n−2) + f(n−3) + f(n−4) 0, 0, 0, 1, 1, 2, 4, 8, 15, 29, 56, 108, ... [5]
5 pentanaccital f(n−1) + ... + f(n−4) + f(n−5) 0, 0, 0, 0, 1, 1, 2, 4, 8, 16, 31, 61, 120, ... [6]
6 hexanaccital f(n−1) + ... + f(n−5) + f(n−6) 0, 0, 0, 0, 0, 1, 1, 2, 4, 8, 16, 32, 63, 125, ... [7]
7 heptanaccital f(n−1) + ... + f(n−6) + f(n−7) 0, 0, 0, 0, 0, 0, 1, 1, 2, 4, 8, 16, 32, 64, 127, ... [8]

För sekvensen av ordning n kan antingen n stycken tvåpotenser eller (n−1) stycken nollor följda av en etta väljas som begynnelsevärden. Flera av de generaliserade fibonaccisekvenserna har intressanta kombinatoriska tolkningar.

Andra objekt än tal

Fibonaccipolynomen är en sekvens av polynom som definieras av

F_n(x)=\left\{\begin{matrix} 1,\qquad\qquad\qquad\qquad&\mbox{om }n=1\\ x,\qquad\qquad\qquad\qquad&\mbox{om }n=2\\ xF_{n-1}(x)+F_{n-2}(x),&\mbox{om }n\ge3 \end{matrix}\right.

De första fibonaccipolynomen är:

F_1(x)=1 \,
F_2(x)=x \,
F_3(x)=x^2+1 \,
F_4(x)=x^3+2x \,
F_5(x)=x^4+3x^2+1 \,
F_6(x)=x^5+4x^3+3x \,

Värdet av det n-te fibonaccipolynomet för x = 1 är lika med det n-te fibonaccitalet.

Om två textsträngar b och a används som begynnelsevärden och addition tolkas som konkatenering fås på liknande sätt sekvensen

b, a, ab, aba, abaab, abaababa, abaababaabaab, ...

Källor

  1. ↑ (talföljd A000045 i OEIS)
  2. ↑ (talföljd A005478 i OEIS)
  3. ↑ (talföljd A001175 i OEIS)
  4. ↑ (talföljd A000073 i OEIS)
  5. ↑ (talföljd A000078 i OEIS)
  6. ↑ (talföljd A001591 i OEIS)
  7. ↑ (talföljd A001592 i OEIS)
  8. ↑ (talföljd A066178 i OEIS)
Hämtad från "https://sv.rilpedia.org/wiki/Fibonaccital"
Personliga verktyg