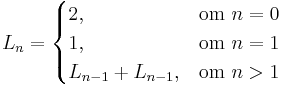Lucastal

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inom talteorin är lucastalen en talsekvens Ln, definierad av:

L_n = \begin{cases} 2,&\mbox{om } n = 0\\ 1,&\mbox{om } n = 1\\ L_{n-1}+L_{n-1},&\mbox{om } n > 1 \end{cases}

De första lucastalen är

2, 1, 3, 4, 7, 11, 18, 29, 47, 76, ... (talföljd A000204 i OEIS)

Lucastalens definition liknar mycket definitionen för fibonaccitalen; skillnaden är att de två första talen är 2 och 1 istället för 0 och 1. Därför visar lucastalen också ett nära släktskap med fibonaccitalen. Till exempel:

  • Ln = Fn − 1 + Fn + 1 om n > 1
  • F2n = FnLn
  • F3n = Fn(L2n + ( − 1)n)
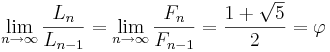
  • \lim_{n\rightarrow\infty}\frac{L_n}{L_{n-1}} = \lim_{n\rightarrow\infty}\frac{F_n}{F_{n-1}} = \frac{1+\sqrt{5}}{2} = \varphi

där Fn är det n-te fibonaccitalet, och φ är det gyllene snittet.

Externa länkar


E-to-the-i-pi.svg Denna matematik-relaterade artikel är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Lucastal"
Personliga verktyg
På andra språk