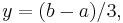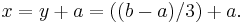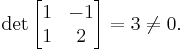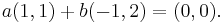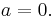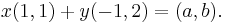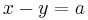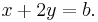Bas (linjär algebra)
Från Rilpedia
En mängd 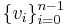 säges vara en bas för ett linjärt rum (eller vektorrum) V om den är linjärt oberoende och spänner upp V, dvs varje element i V kan uttryckas som en linjärkombination av element ur basen.
säges vara en bas för ett linjärt rum (eller vektorrum) V om den är linjärt oberoende och spänner upp V, dvs varje element i V kan uttryckas som en linjärkombination av element ur basen.
En basvektor 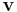 i ett vektorrum V med dimension d, är en vektor i den mängd av d stycken vektorer som bildar en bas för rummet. Basvektorerna är linjärt oberoende.
i ett vektorrum V med dimension d, är en vektor i den mängd av d stycken vektorer som bildar en bas för rummet. Basvektorerna är linjärt oberoende.
Baser av stor betydelse är de som är ortogonala eller ortonormerade.
Innehåll |
Hur man visar att en mängd vektorer är en bas
För detta exempel betrakta vektorerna (1,1) och (-1,2), som vi vill visa är en bas för R2. Vi skall visa att de är linjärt oberoende, och att de spänner upp hela rummet. Det finns många sätt att göra detta.
Med hjälp av dimensionssatsen
Enklast ser vi att eftersom (-1,2) inte är en multipel av (1,1), och eftersom (1,1) inte är nollvektorn, är de linjärt oberoende, och därmed också en bas för R2 eftersom vi vet att dimensionen är 2. Detta är en konsekvens av dimensionssatsen. VSV
Med matrisinvers, determinanter
Beräkna determinanten
Eftersom matrisen ovan har en determinant som inte är 0, bildar kolumnvektorerna en bas för R2. VSV
En tredje metod
Vi börjar med att visa att vektorerna är linjärt oberoende. Antag att det finns skalärer a och b, som uppfyller ekvationen
Det gäller alltså att:
-
alltså är
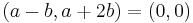 och
och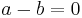
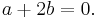
Subtraherar vi nu den första ekvationen från den andra får vi:
-
så
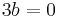
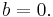
Och sedan från den första ekvationen att:
Vi visar nu att hela R2 spänns upp. Vi låter (a,b) beteckna en godtycklig vektor i rummet, och visar att det finns skalärer x och y som uppfyller att:
Vi måste alltså lösa ekvationssystemet:
Drar vi den första ekvationen från den andra får vi:
-
och sen
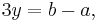
-
och slutligen