Linjärt oberoende

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Linjärt oberoende är ett centralt begrepp inom linjär algebra. En familj av vektorer sägs vara linjärt oberoende om ingen av dem kan uttryckas som en ändlig linjärkombination av de övriga.

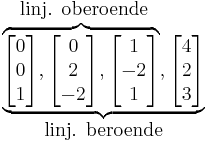
Exempelvis har vi i 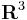\mathbf{R}^3 följande exempel:

\begin{matrix} \mbox{linj. oberoende}\qquad\\ \underbrace{ \overbrace{ \begin{bmatrix}0\\0\\1\end{bmatrix}, \begin{bmatrix}0\\2\\-2\end{bmatrix}, \begin{bmatrix}1\\-2\\1\end{bmatrix} }, \begin{bmatrix}4\\2\\3\end{bmatrix} }\\ \mbox{linj. beroende}\\ \end{matrix}

Vi ser här att de första tre vektorerna är linjärt oberoende, men att den fjärde vektorn kan skrivas som 9 gånger den första plus 5 gånger den andra plus 4 gånger den tredje vektorn. Alltså är de fyra vektorerna ej linjärt oberoende. Man säger då att de är linjärt beroende, och man kan visa att vilken som helst av de fyra linjärt beroende vektorerna kan skrivas som en linjärkombination av de tre övriga.

Definition

Låt 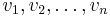v_1, v_2, \ldots, v_n vara element i något vektorrum V. Vektorerna sägs nu vara linjärt oberoende om det gäller att ekvationen 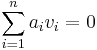\sum_{i=1}^n a_i v_i = 0 endast har den triviala lösningen a_1 = a_2 = \ldots = a_n = 0

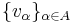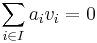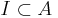Mera allmänt gäller att en familj av vektorer \{v_{\alpha}\}_{\alpha \in A} där A är en godtycklig indexmängd är linjärt oberoende om ekvationen \sum_{i \in I} a_i v_i = 0 , där I \subset A är en ändlig delmängd av A, bara har den triviala lösningen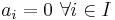 a_i = 0 \,\, \forall i \in I

En mängd vektorer som är linjärt oberoende och som spänner upp ett visst vektorrum sägs utgöra en bas för vektorrummet.

Exempel

För att bestämma huruvida en familj av vektorer är linjärt oberoende finns det flera sätt att gå tillväga. Ett sätt är att uttnyttja definitionen genom att ställa upp ekvationssystemet 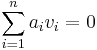\sum_{i=1}^n a_i v_i = 0 och undersöka dess lösningar. Finns icke-triviala lösningar är familjen linjärt beroende, annars linjärt oberoende.

För ett ändligtdimensionellt vektorrum V gäller alltid att 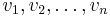v_1, v_2, \ldots, v_n är linjärt beroende om n > dim V, dimensionen av V.

Det gäller även att en mängd vektorer är linjärt beroende omm en av vektorerna kan skrivas som en linjärkombination av de övriga.

Har man en familj 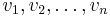v_1, v_2, \ldots, v_n i ett vektorrum av dimension n, kan man avgöra om familjen är linjärt oberoende genom att bilda en matris av dessa (uttryckta i någon bas). Det gäller nämligen att vektorerna är linjärt oberoende omm matrisens determinant är skild från 0.

Referenser

  • S. Axler, Linear Algebra Done Right, Springer Verlag, 1996
  • G. Sparr, Linjär Algebra, Studentlitteratur, 1994
Hämtad från "https://sv.rilpedia.org/wiki/Linj%C3%A4rt_oberoende"
Personliga verktyg