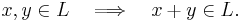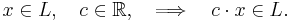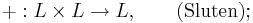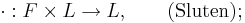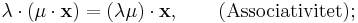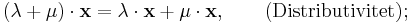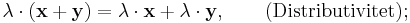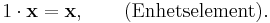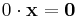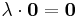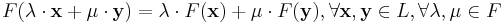Linjärt rum

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Matematiska begrepp

Innehåll

Informell definition

Ett linjärt rum (även kallat ett vektorrum) är en mängd med en 'linjär struktur'.

Om man tar två element ur mängden, så kan man sammanfoga dem (addera dem) till ett nytt element, som även det ligger i mängden:

x,y \in L \quad \Longrightarrow \quad x+y \in L.

Man kan även ta ett element ur mängden och 'multiplicera' det med ett tal. Då bildas ett nytt element som även det ligger i mängden.

x \in L, \quad c \in \mathbb{R}, \quad \Longrightarrow \quad c \cdot x \in L.

(På 'matematiska' säger man att 'mängden är sluten under addition och multiplikation med skalärer'.)

'Sammanfogningen' ( + ) och 'multiplikationen' (\cdot) har samma egenskaper som vanlig addition med tal och multiplikation med tal.

Matematisk definition

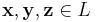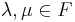Ett linjärt rum, även lineärt rum eller vektorrum, är en mängd L tillsammans med en kropp F där addition ( + ) och multiplikation (\cdot) är definierade så att följande axiom är uppfyllda för alla \mathbf{x},\mathbf{y},\mathbf{z}\in L och \lambda,\mu\in F.

I. Addition

+ : L \times L \rightarrow L, \qquad \rm{(Sluten)};
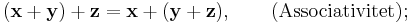
  1. (\mathbf{x}+\mathbf{y})+\mathbf{z}=\mathbf{x}+(\mathbf{y}+\mathbf{z}), \qquad \rm{(Associativitet)};
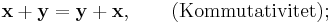
  2. \mathbf{x}+\mathbf{y}=\mathbf{y}+\mathbf{x}, \qquad \rm{(Kommutativitet)};
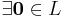  3. \exist \mathbf{0} \in L så att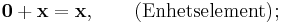 \mathbf{0}+\mathbf{x}=\mathbf{x}, \qquad \rm{(Enhetselement)};
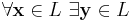  4. \forall \mathbf{x} \in L \ \exist \mathbf{y} \in L så att \mathbf{x}+\mathbf{y}=\mathbf{0}, \qquad \rm{(Invers)}.

II. Skalärmultiplikation

\cdot : F \times L \rightarrow L, \qquad \rm{(Sluten)};
  1. \lambda\cdot(\mu\cdot\mathbf{x})=(\lambda\mu)\cdot\mathbf{x}, \qquad \rm{(Associativitet)};
  2. (\lambda+\mu)\cdot\mathbf{x}=\lambda\cdot\mathbf{x}+\mu\cdot\mathbf{x}, \qquad \rm{(Distributivitet)};
  3. \lambda\cdot(\mathbf{x}+\mathbf{y})=\lambda\cdot\mathbf{x}+\lambda\cdot\mathbf{y}, \qquad \rm{(Distributivitet)};
  4. 1\cdot\mathbf{x}=\mathbf{x}, \qquad \rm{(Enhetselement)}.


Elementen i mängden L kallas vektorer och elementen i mängden F kallas skalärer.
Med ovanstående axiom kan man sedan visa att

0\cdot\mathbf{x}=\mathbf{0}
\lambda\cdot\mathbf{0}=\mathbf{0}

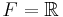Om F=\mathbb{R} så kallas det linjära rummet reellt; om 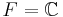F=\mathbb{C} så är det komplext. Man brukar även tala om dimensionen av ett linjärt rum vilket är kardinaliteten på en bas till rummet. En bas till ett linjärt rum är en delmängd av rummet sådan att varje vektor kan, på ett unikt sätt, skrivas som en linjärkombination av vektorer från basen. Vektorerna i en bas kallas även för basvektorer. 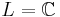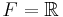Tex om L = F blir dimensionen 1 men om L=\mathbb{C} och F=\mathbb{R} blir dimensionen 2. Varje linjärt rum med ändlig dimension n är isomorft med Fn där F är kroppen.
Att man säger att operationen (+) och (*) är sluten, innebär ovan att
vektorerna x och y ∈ L medför till att (x+y) ∈ L, ∀ x och y ∈ L. Likvärdigt gäller för (*) där skalären a ∈ kroppen F och vektorn x ∈ L ger att produkten a*x ∈ L självt för ∀ a och x
Det är också p.g.a av detta som ofta gör att det blir väldigt beständigt och krångligt att bevisa oändliga linjära rum verkligen uppfyller denna egenskap eller alla axiom, och man brukar ofta då välja ut ett delrum, dvs en mindre delmängd av dessa, vilket gör att det då istället räcker att man behöver uppfylla följande linjära egenskap

F ( \lambda\cdot\mathbf{x} + \mu\cdot\mathbf{y} ) = \lambda\cdot F(\mathbf{x}) + \mu\cdot F(\mathbf{y}), \forall \mathbf{x},\mathbf{y}\in L,\forall \lambda,\mu\in F


och samt att nollvektorn existerar i detta rum.


Exempel

Klicka på bilden för att läsa ett exempel

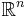\mathbb{R}^n som ett reellt linjärt rum där vektorerna är definierade som n-tiplar av reella tal.

Mängden av alla kontinuerliga funktioner 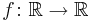f\colon\mathbb{R}\rightarrow\mathbb{R} - en mängd som oftast betecknas C0 - är också ett linjärt rum, men med oändlig dimension.

Se även


Ämnen inom matematik relaterade till rummet:

 Redigera
Topologi | Geometri | Trigonometri | Algebraisk geometri | Differentialgeometri | Algebraisk topologi | Linjär algebra | Fraktal geometri | Kompakt rum
Hämtad från "https://sv.rilpedia.org/wiki/Linj%C3%A4rt_rum"
Personliga verktyg