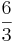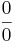Delbarhet
Från Rilpedia
Ett heltal a är delbart med ett annat heltal b om det finns ett heltal k så att a = b·k. Man säger också att "b är en delare (eller divisor) i a" eller att "b delar a". I dagligt tal säger man att a är jämnt delbart med b.
Att b delar a skrivs ofta b|a.
Delbarhet är en matematisk relation och bör inte sammanblandas med operation (kompositionsregeln) "delat med", division. Utsagan
- 3 | 6
är en sann utsaga, därför att det finns minst ett heltal, nämligen talet 2, som multiplicerat med 3 ger produkten 6. Uttrycket
har värdet 2, därför att 2 är det enda tal som multiplicerat med 3 ger produkten 6. Likaså är utsagan
- 0 | 0
en sann utsaga, därför att det finns minst ett heltal (till exempel talet 2867) som multiplicerat med 0 ger produkten 0. Däremot har uttrycket
inte något definierat värde. Division med noll som divisor är förbjudet; men delbarhet med noll som delare är helt accepterat.
Exempel:
- 5|15, eftersom 15 = 5·3
- (-5)|15, eftersom 15 = (-5)·(-3)
- b|0 för alla b, eftersom 0 = b·0
- a|a för alla a, eftersom a = a·1
Enkla satser om delbarhet (gäller för alla heltal a, b, c, x, y):
- Om a|b, så a|bc
- Om a|b och a|c, så a|(b+c)
- Om a|b och a|c, så a|(xb+yc)
Om a och b är positiva heltal och a | b, så är värdet av uttrycket 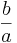 ett positivt heltal, och
ett positivt heltal, och 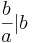 . Detta medför att b har ett udda antal positiva delare omm
. Detta medför att b har ett udda antal positiva delare omm 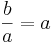 för något positivt heltal a, alltså omm b är en heltalskvadrat.
för något positivt heltal a, alltså omm b är en heltalskvadrat.