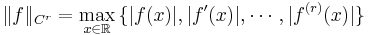Norm (matematik)

Från Rilpedia

(Omdirigerad från Vektornorm)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Manhattan-normen (röd, blå, gul) och euklidisk norm (grön)

Inom matematiken är norm ett sätt att tilldela en längd till objekt definierade i ett vektorrum. Normen, ofta betecknad med ||  || uppfyller följande villkor, där x och y tillhör ett vektorrum X och a är en skalär:

  • ||x|| = 0 omm x = 0
  • ||a x||  =  |a| ||x||
  • ||x + y|| ≤ ||x|| + ||y||

Det är dock inte säkert att det går att tilldela varje vektorrum en norm; om det är möjligt så kallas vektorrummet ifråga för ett normerat rum. Om ett normerat rum dessutom är fullständigt (med avseende på metriken som induceras av normen), så kallas det för ett Banachrum.

En seminorm eller pseudonorm är en funktion som tillåts avbilda nollskilda element på noll, men som i övrigt uppfyller villkoren för en norm.

Innehåll

Exempel i ändligdimensionella rum

Rn kan ha ett flertal olika normer, några exempel (här är x = (x1, ... , xn), där varje xi tillhör R. I Cn blir det inte stor skillnad; följande normer fungerar även där. (Det är därför som beloppstecken alltid är utsatta runt x).

Euklidisk norm

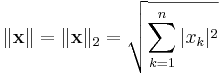
\|\mathbf{x}\| = \|\mathbf{x}\|_2 = \sqrt{\sum_{k=1}^{n}|x_k|^2}

Den euklidiska normen kan ses som en generalisering av Pythagoras sats i flera dimensioner.

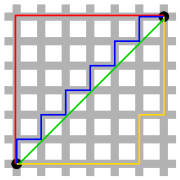
'Manhattan-normen'

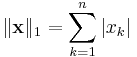
\|\mathbf{x}\|_1 = \sum_{k=1}^{n}|x_k|

p-norm

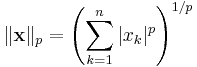
\|\mathbf{x}\|_p = \left(\sum_{k=1}^{n}|x_k|^p\right)^{1/p}

Manhattan-normen och den Euklidiska normen fås som specialfall (p=1 resp 2)

Maximumnormen

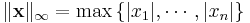
\|\mathbf{x}\|_\infty = \max{\{|x_1|, \cdots ,|x_n|\}}

Exempel i oändligdimensionella rum

Ett exempel på ett oändligdimensionellt rum är rummet av alla funktioner, säg från R till R. Några exempel på normer definierade i delrum av detta:

Cr-norm

Betrakta delrummet av r gånger kontinuerligt deriverbara funktioner.

\|f\|_{C^r} = \max_{x \in \mathbb{R}} {\{|f(x)|, |f'(x)|, \cdots ,|f^{(r)}(x)|\}}

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Norm_(matematik)"
Personliga verktyg