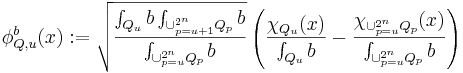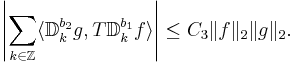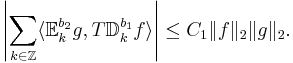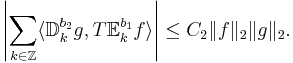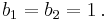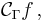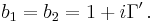Tb-satsen
Från Rilpedia
Tb-satsen är en matematisk sats som säger att en viss singulär integraloperator, T, är en begränsad operator 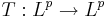 om och endast om man kan definiera T för en vissa funktion b1 och man kan definiera T:s transponat T* för en viss funktion b2. Satsen säger då att man måsta testa operatorn T och transponatet T* för endast dessatvå funktioner b1 och b2.
om och endast om man kan definiera T för en vissa funktion b1 och man kan definiera T:s transponat T* för en viss funktion b2. Satsen säger då att man måsta testa operatorn T och transponatet T* för endast dessatvå funktioner b1 och b2.
Guy David, Jean-Lin Journé och Stephen Semmes bevisade Tb-satsen 1985.
Innehåll |
Bakgrund
En linjär operator T som opererar på mätbara funktioner i  är en integraloperator om det finns en kärna
är en integraloperator om det finns en kärna 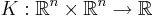 så att man kan formulera
så att man kan formulera
för en funktion f och alla 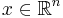 . Tyvärr är ofta den här formeln inte definierad för alla funktioner och inte heller för alla punkter. De här operatorerna kallas singulära. Mer precist, en integraloperator T är en singulär integraloperator om kärnan K inte är definierad inom diagonalen
. Tyvärr är ofta den här formeln inte definierad för alla funktioner och inte heller för alla punkter. De här operatorerna kallas singulära. Mer precist, en integraloperator T är en singulär integraloperator om kärnan K inte är definierad inom diagonalen
och Tf(x) är definierad bara när
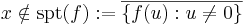 ,
,
dvs Tf(x) är inte definierad i funktionens f underlag.
Den intressanta frågan är: hur kan vi definiera en singulär integraloperator så att den är en begränsad operator 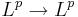 där
där 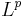 är Lp-rummet för
är Lp-rummet för  ?
?
Hilberttransform
Till exempel, låt 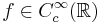 , dvs underlaget för f är en kompakt mängd och f är
, dvs underlaget för f är en kompakt mängd och f är 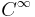 . Definiera
. Definiera
för 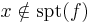 , dvs
, dvs 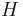 är Hilberttransformen. Då blir kärnan
är Hilberttransformen. Då blir kärnan
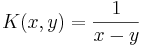 .
.
Hilberttransformen är en singulär integraloperator eftersom kärnan har en singulär punkt när 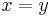 . Man kan också definiera Hilbertransformen för Lp-funktioner eftersom
. Man kan också definiera Hilbertransformen för Lp-funktioner eftersom 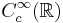 är en tät delmängd i
är en tät delmängd i 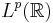 .
.
Dessutom, med detta kan man visa att det finns 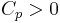 så att om
så att om 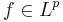 så är
så är
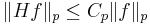 .
.
Därför är H en begränsad operator 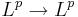 .
.
Kan man även visa detta för generella singulära integraloperatorer? Tb-satsen förklarar att det går.
Antaganden
Inom Tb-satsen behövs några antaganden om testfunktionerna b1 och b2, kärnan K och operatoren T.
Para-akkretivt antagande för testfunktionen
Låt 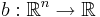 vara en lokalt integrebar funktion. Man sägar att b är en para-akkretiv funktion om det finns
vara en lokalt integrebar funktion. Man sägar att b är en para-akkretiv funktion om det finns 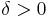 så att
så att
för alla kuber 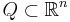 där integralen är Lebesgueintegralen och |Q| är kubens Q:s Lebesguemått.
där integralen är Lebesgueintegralen och |Q| är kubens Q:s Lebesguemått.
Standardvillkor för kärnan
En kärna 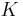 är en Calderón-Zygmund kärna om det uppfyller standardvillkoren:
är en Calderón-Zygmund kärna om det uppfyller standardvillkoren:
- Begränsadvillkor: det finns
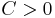 så att
så att
- för alla
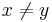 .
.
- Tillväxtvillkor: det finns
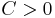 och
och 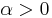 så att
så att
- för alla
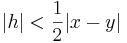 .
.
Svagt begränsat-villkor för operatorer
Låt 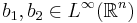 vara para-akkretiva funktioner. En linjär operator T är
vara para-akkretiva funktioner. En linjär operator T är 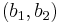 -svagt begränsat om det finns
-svagt begränsat om det finns 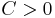 så att
så att
för alla kuber 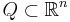 .
.
Begränsad med mellansvängning (rummet BMO)
Man behöver också funktioner som är begränsade med mellansvängning. En lokalt integrebar funktion 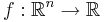 är begränsad med mellansvängning (eng. Bounded with Mean Oscillation) om det finns
är begränsad med mellansvängning (eng. Bounded with Mean Oscillation) om det finns 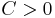 så att
så att
för alla kuber 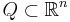 . Om en funktion
. Om en funktion 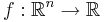 är begränsad med mellansvängning skriver man
är begränsad med mellansvängning skriver man
Tb-satsen
Låt 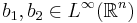 vara para-akkretiva funktioner, dessa kallas testfunktioner. Låt
vara para-akkretiva funktioner, dessa kallas testfunktioner. Låt 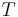 vara en integraloperator som har en Calderón-Zygmund kärna. Antag att
vara en integraloperator som har en Calderón-Zygmund kärna. Antag att 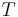 är definierad för
är definierad för 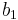 och dessutom
och dessutom 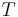 :s transponat
:s transponat 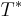 är definierad för
är definierad för 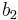 .
.
Då är 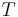 en begränsad operator
en begränsad operator 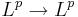 om och endast om
om och endast om
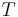 är
är 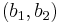 -svagt begränsad,
-svagt begränsad,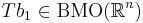 och
och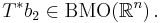
Skiss av bevis
Vår idé är att vi första prova Tb-satsen så att vi har en begränsad operator 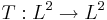 . Det här är den kritiska andelen för det här provet. Nämligen, när vi har
. Det här är den kritiska andelen för det här provet. Nämligen, när vi har 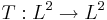 det är lätt att prova
det är lätt att prova 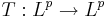 för fixt
för fixt 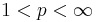 eftersom vi kan interpolate med Cotlars olikheten för
eftersom vi kan interpolate med Cotlars olikheten för 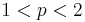 och sedan använda dualhetet för
och sedan använda dualhetet för 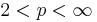 .
.
Nuförtiden där finns många olika bevis för 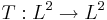 . En prov är att vi använda dyadisk kuber:
. En prov är att vi använda dyadisk kuber:
Om 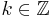 så är
så är 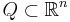 en dyadisk kub med ordning k, om där finns
en dyadisk kub med ordning k, om där finns 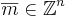 så att
så att
Vi betäckna 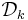 av familj av alla dyadisk kuber med ordning k i
av familj av alla dyadisk kuber med ordning k i  och
och
För varje 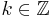 dyadiska kuber med ordning k är en stratifiering av
dyadiska kuber med ordning k är en stratifiering av  och vi har:
och vi har:
Vi har en begränsad operator 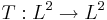 om och endast om vi kan bevisa att
om och endast om vi kan bevisa att
för alla 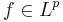 . Eftersom
. Eftersom 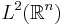 är en Hilbertrummet med inre produkten
är en Hilbertrummet med inre produkten
så man kan använda inom funktionalanalys så att
Därför, vi måste använda att
för alla 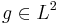 och
och 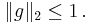
För 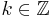 och en para-akkretiv funktion
och en para-akkretiv funktion 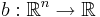 definiera sannolikhetsteoretiska begrepper "väntevärder" och "spridninger":
definiera sannolikhetsteoretiska begrepper "väntevärder" och "spridninger":
- k-väntevärde:
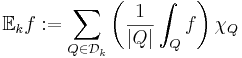
- k-spridning:
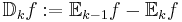
- b-viktad k-väntevärde:
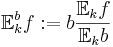
- b-viktad k-spridning:
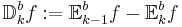
Med Carlesons inbäddningsats vi kan visa att
för 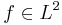 med konvergens vid L2-norm. Med svagt begränsat-villkor och standardvillkor man kan visa att för
med konvergens vid L2-norm. Med svagt begränsat-villkor och standardvillkor man kan visa att för 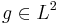 med
med 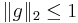 vi har
vi har
Å andra sidan för en para-akkretiv funktion b, en dyadisk kub 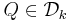 ,
, 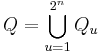 , var
, var 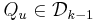 , och
, och 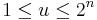 definirar vi en Haarfunktion
definirar vi en Haarfunktion 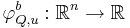 så att
så att
- Med Haarfunktioner man kan använda b-viktad k-väntevärder och -spridningar så att man har:
- Med BMO-rummets tillämpningar, paraprodukter, Carlesons inbäddningsats och liten dyadisk analys man har:
- Förra är symmetrisk med
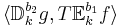 , dvs man har:
, dvs man har:
Därför vi har med triangelolikheten att
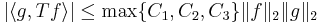 ,
,
dvs Tb-satsen.
Tillämpningar
- Hilberttransformen
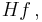
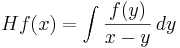 ,
,
är en begränsad operator 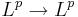 eftersom man kan testa Hilbertransformen med para-akkretiva testfunktioner
eftersom man kan testa Hilbertransformen med para-akkretiva testfunktioner
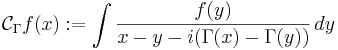 ,
,
är en begränsad operator 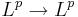 eftersom man kan testa Cauchytransformen med para-akkretiva testfunktioner
eftersom man kan testa Cauchytransformen med para-akkretiva testfunktioner
Här 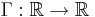 är en Lipschitzfunktion vilket ger att derivatan
är en Lipschitzfunktion vilket ger att derivatan 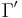 finns nästan överallt.
finns nästan överallt.
Se även
Referenser
- Guy David, Jean-Lin Journé, Stephen Semmes, Opérateurs de Calderón-Zygmund, fonctions para-accrétives et interpolation, Rev. Mat. Iberoamericana 1(4): 1 - 56, 1985.




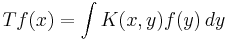
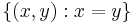
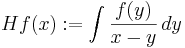
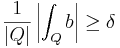
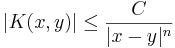
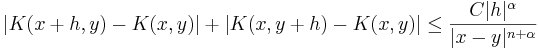
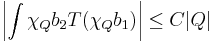
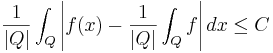
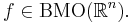
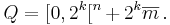
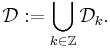
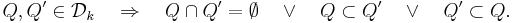
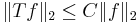
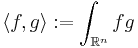
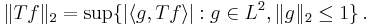
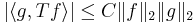
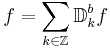
![|\langle g,Tf \rangle | = \left|\sum_{k \in \Z} \langle g,[(\mathbb{E}_k^{b_2})^* T \mathbb{D}_k^{b_1} + (\mathbb{D}_k^{b_2})^* T \mathbb{E}_k^{b_1} + (\mathbb{D}_k^{b_2})^* T \mathbb{D}_k^{b_1} ]f \rangle \right| .](/w/images/sv.rilpedia.org/math/5/e/9/5e962e6b4d4e9748e89cb731aac2e617.png)