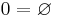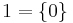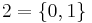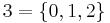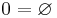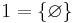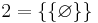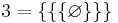Tal (matematik)
Från Rilpedia
Denna artikel behandlar tal såsom matematiskt begrepp. För andra betydelser, se tal.
| Matematiska begrepp |
|---|
Tal är ett matematiskt grundbegrepp som används för att representera olika storheter, det vill säga sådant som går att mäta i bestämda måttenheter, till exempel antal, längd, vikt, volym, temperatur och tryck. Ett tal är en abstrakt enhet som representerar ett antal eller ett mått. I matematik, är definitionen av tal vidare och inkluderar exempelvis bråk, negativa tal, irrationella tal, transcendenta tal och komplexa tal.
Innehåll |
Typer av tal
Naturliga tal är beskrivna redan i förhistorien. Rationella tal, som är kvoter av heltal, uppkom under antiken. Algebraiska tal är tal som kan definieras utifrån ett ändlig uttryck med rationella tal. Transcendentala tal är alla övriga reella tal.
Naturliga tal
De naturliga talen är alla heltal som inte är negativa {0, 1, 2, 3 ...} eller alla positiva heltal {1, 2, 3, 4 ...}. De brukar betecknas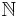 
.
Heltal
Negativa tal är motsatsen till de positiva talen. De skrivs oftast med ett minustecken framför så att -3 är motsatsen till 3. Kombinerar man de negativa heltalen, nollan och de positiva heltalen så får man heltalen, som betecknas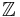 
efter det tyska ordet zahl.
Rationella tal
De rationella talen är kvoter av heltal, de kan alltså skrivas som bråk av heltal. De rationella talen var av stor betydelse för babylonerna och egyptierna. Mängden av alla rationella tal betecknas ofta med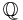 
.
Informell diskussion
I meningen "Fem myror är fler än fyra elefanter." är det inte fråga om en jämförelse av storleken hos myror och elefanter, utan det är antalet element i 'Myr-mängden' som är större än antalet element i 'Elefant-mängden'. Här är man inte intresserad av att en elefant har mycket större kroppshydda än en myra, även om det kanske är just kroppshyddan som andra först tänker på när de jämför myror med elefanter.
På samma sätt är tusen enkronors-mynt fler än en tusenkronors-sedel. Däremot är tusen enkronors-mynt värda lika mycket som en tusenkronors-sedel. Här är det en fråga om två olika mått av de två mängderna "Tusen enkronors-mynt" och "en tusenkronorssedel": Det ena måttet, räknemåttet, ger upplysning om antalet element i en mängd, medan det andra måttet, värdemåttet, anger värdet (här i kronor) räknat av elementen i en mängd, i den mån det går att mäta mängden med ett sådant mått.
Formell diskussion
Man kan definiera de så kallade naturliga talen 0,1,2,3,..., genom att först definiera talet noll (0) som den tomma mängden
och därefter successivt definiera de andra naturliga talen på följande sätt:
Ett annat sätt att definiera de naturliga talen är att imitera de ryska så kallade matrjosjka-dockorna, där det inuti varje docka finns en mindre docka. Till skillnad från den ryska matrjosjka-dockan, innehåller den matematiska matrjosjka-dockan oändligt många dockor:
Bakom de tre punkterna som utgör ellipsis-symbolen (...) i uppräkningen av de naturliga talen 0,1,2,3,..., ligger den så kallade Principen om matematisk induktion; I de två listorna ovan kan man se ett mönster i konstruktionerna av talen 0,1,2 och 3. Principen om matematisk induktion låter oss hävda att om vi fortsätter detta mönster i all oändlighet, så har vi lyckats konstruera de naturliga talen.
Se även
- Wikimedia Commons har media som rör Tal (matematik)
Olika typer av matematiska tal
Naturliga tal - Heltal - Positiva tal - Noll - Negativa tal - Rationella tal - Irrationella tal - Reella tal - Algebraiska tal - Transcendent tal - Imaginära tal - Komplexa tal - Hyperkomplexa tal (Kvaternioner Oktonioner Sedenioner) - Perfekta tal
