Mängd
Från Rilpedia
| Matematiska begrepp |
|---|
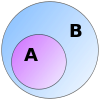
En mängd är en samling av objekt. De objekt som ingår i en mängd kallas mängdens element. I axiomatisk mängdteori, till exempel ZFC, finns ett antal axiom som fastställer hur mängder får bildas. De får till exempel inte ha sig själva som element. Men i stort sett är det nästan inga begränsningar på vad en mängd får innehålla.
En mängd är ändlig eller oändlig beroende på om den innehåller ett ändligt eller oändligt antal element. Ändliga mängder kan anges genom att man räknar upp elementen inom klammrar; exempelvis {2, 3, 5, 7} är mängden av alla primtal under 10. Mängden av alla primtal är emellertid oändlig (det finns oändligt många primtal), så den kan man inte ange på detta sätt. Ett mer generellt sätt att ange mängder är genom att skriva {x : A(x)}, vilket betyder mängden av alla x som har egenskapen A (märk att andra tecken än kolon kan användas i litteraturen). Till exempel kan mängden av samtliga primtal skrivas {x : x är ett primtal}. Nästan alla matematiska begrepp som finns kan reduceras till mängder.
Två mängder är lika om de innehåller exakt samma element. Mängder är oordnade dvs det spelar ingen roll i vilken ordning vi räknar upp elementen. {1, 2, 3} = {3, 1, 2}. Det spelar heller ingen roll om vi räknar upp några element flera gånger. {1, 1, 2, 3} = {1, 2, 3, 3, 3, 3}.
Den mängd som inte innehåller några element alls skrivs {} eller ∅ och kallas den tomma mängden. Den mängd som innehåller alla element som är relevanta (dvs alla element som ingår i domänen för det man för tillfället studerar) kallas universum, universalmängd eller "grundmängd" och betecknas ibland med bokstaven U eller G.
Vanliga mängdoperationer är:
- Unära: komplement, potensmängd
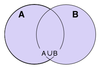
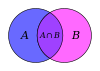
- Binära: snitt, union, differens, produkt
Två mängder A och B sägs innehålla lika många element om och endast om det finns en bijektiv funktion från A till B. Exempelvis finns det ingen sådan från de naturliga talen till de reella och därför kan man säga att det finns fler reella tal än naturliga.
Antalet element i en mängd betecknas med absolutbelopp, ex: |M| och kallas mängdens kardinaltal. Mängden av alla naturliga tal , 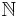 , har kardinaltalet Alef-noll som är den minsta oändliga kardinaliteten.
, har kardinaltalet Alef-noll som är den minsta oändliga kardinaliteten.
Mängdegenskaper
Några kända talmängder:
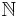 , mängden av naturliga tal
, mängden av naturliga tal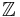 , mängden av hela tal
, mängden av hela tal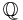 , mängden av rationella tal
, mängden av rationella tal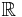 , mängden av reella tal
, mängden av reella tal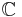 , mängden av komplexa tal
, mängden av komplexa tal
Se även: