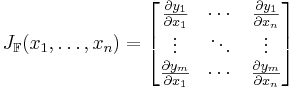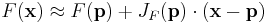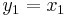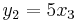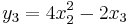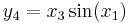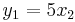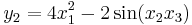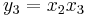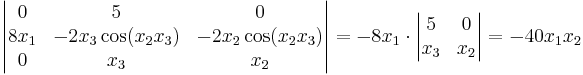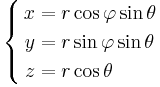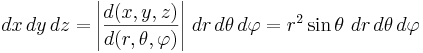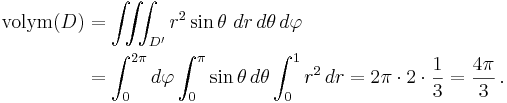Jacobimatris

Från Rilpedia

Texten från svenska Wikipedia

Jacobimatris (också kallad Jacobian eller funktionalmatris), efter Carl Gustav Jakob Jacobi, är en matris bestående av olika partialderivator som tillhör ett system av funktioner. Tillsammans med dess determinant (jacobideterminanten) används den inom vektoranalysen. Både matrisen och dess determinant kan ibland något slarvigt benämnas jacobian.

Jakobimatris

Jacobimatrisen är en matris innehållande alla första ordningens partiella derivator för en vektorvärd funktion, och är av betydelse då den representerar den bästa linjäraapproximationen av en differentierbar funktion i en omgivning till en given punkt. Jakobimatrisen kan därmed ses som en motsvarighet till derivata för vektorvärda funktioner.

Låt 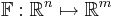$\mathbb{F}: \R^n \mapsto \R^m$ vara en funktion från ett Euklidiskt rum av dimension n till ett Euklidiskt rum av dimension m. En sådan funktion ges av m reella funktioner, $y_1(x_1,\dots,x_n), \dots, y_m(x_1,\dots,x_n)$ . Om de existerar kan de partiella derivatorna av dessa funktioner ordnas i en 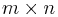$m\times n$ -matris, alltså 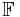$\mathbb{F}$ Jacobimatris 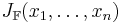$J_\mathbb{F}(x_1,\ldots,x_n)$ , enligt:

$J_\mathbb{F}(x_1,\ldots,x_n)=\begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_n} \end{bmatrix}$

Ett alternativt skrivsätt är 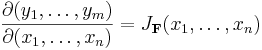$\frac{\partial(y_1,\ldots,y_m)}{\partial(x_1,\ldots,x_n)}=J_\mathbf{F}(x_1,\ldots,x_n)$

Matrisens i:e rad ges alltså av gradienten till $y i$ .

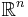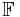Om p är en punkt i $\R^n$ och $\mathbb{F}$ är differentierbar i p, så ges dess derivata av 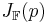$J_\mathbb{F}(p)$ . Här kommer den linjära transformation som beskrivs av 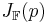$J_\mathbb{F}(p)$ vara den bästa möjliga approximationen av 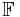$\mathbb{F}$ i en omgivning till p, i meningen att

$F(\mathbf{x}) \approx F(\mathbf{p}) + J_F(\mathbf{p})\cdot (\mathbf{x}-\mathbf{p})$

för x nära p.

Exempel

Följande funktion betecknar ett variabelbyte från sfäriska koordinater till kartesiska koordinater:

$\mathbb{F}: \R^+ \times [0,2\pi)\times [0,\pi]\mapsto \R^3$ .

Mer explicit skrivs den

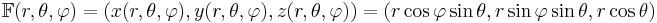$\mathbb{F}(r,\theta,\varphi)=(x(r,\theta,\varphi),y(r,\theta,\varphi), z(r,\theta,\varphi))=(r \cos\varphi \sin\theta, r \sin\varphi \sin\theta, r \cos\theta)$ .

Jacobimatrisen för detta variabelbyte är

$J_\mathbb{F}(r,\varphi,\theta) =\begin{bmatrix} \cos\varphi \sin\theta & -r \sin\varphi \sin\theta & r \cos\varphi \cos\theta \\ \sin\varphi \sin\theta & r \cos\varphi \sin\theta & r \sin\varphi \cos\theta \\ \cos\theta & 0 & -r \sin\theta \end{bmatrix}$ .

Jacobimatrisen för funktionen $\mathbb{F}: \R^3\mapsto \R^4$ med komponenter

$y_1 = x_1 \,$

$y_2 = 5x_3 \,$

$y_3 = 4x_2^2 - 2x_3 \,$

$y_4 = x_3 \sin(x_1) \,$

är

$J_F(x_1,x_2,x_3) =\begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 5 \\ 0 & 8x_2 & -2 \\ x_3\cos(x_1) & 0 & \sin(x_1) \end{bmatrix}$ ,

vilket visar att jacobimatrisen inte behöver vara kvadratisk.

Jakobideterminanten

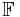Om $m = n$ , det vill säga $\mathbb{F}$ är en funktion från ett n-dimensionellt rum till ett annat n-dimensionellt rum, så är Jacobimatrisen kvadratisk, och därmed är dess determinant väldefinierad. Denna kallas jacobideterminanten, och dess värde i en punkt ger viktig information om funktionen i denna omgivning. Om $\mathbb{F}$ är kontinuerligt differentierbar är den även inverterbar i närheten av p om Jacobideterminanten är nollskild i p. Om determinanten är positiv i p bevarar $\mathbb{F}$ orientering, och om den är negativ skiftar $\mathbb{F}$ orientering. Vidare ger absolutvärdet av Jacobideterminanten i p den faktor med vilken 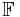$\mathbb{F}$ skalar om area/volym/hypervolym i närheten av p. Detta används i variabelsubstitution.

Exempel

Jakobideterminanten för funktionen 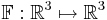$\mathbb{F}: \R^3 \mapsto \R^3$

med komponenterna

$y_1 = 5x_2 \,$

$y_2 = 4x_1^2 - 2 \sin (x_2x_3) \,$

$y_3 = x_2 x_3 \,$

är

$\begin{vmatrix} 0 & 5 & 0 \\ 8x_1 & -2x_3\cos(x_2 x_3) & -2x_2\cos(x_2 x_3) \\ 0 & x_3 & x_2 \end{vmatrix}=-8x_1\cdot\begin{vmatrix} 5 & 0\\ x_3&x_2\end{vmatrix}=-40x_1 x_2$

Vi kan av detta dra slutsatsen att 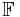$\mathbb{F}$ kastar om orienteringen i närheten av alla punkter där $x 1$ och $x 2$ har samma tecken, och att funktionen är lokalt inverterbar överallt utom i $x 1 = 0$ eller $x 2 = 0$ . Ett litet objekt som befinner sig i närheten av (1,1,1) som mappas om av 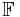$\mathbb{F}$ kommer öka sin volym cirka 40 gånger.

Användningar

Jakobideterminanten används när man gör variabelbyten när man integrerar en funktion för att kompensera för basbytet. Den kommer då dyka upp som en multiplikativ term under integraltecknet. Det är vanligtvis nödvändigt att variabelbytet är injektivt, vilket gör att jakobideterminanten är väldefinierad.

Exempel

Följande demonstrerar en användning av jakobideterminanten vid beräkning av en integral. Antag att man vill beräkna volymen av enhetssfären $x 2 + y 2 + z 2 = 1$ . Låt 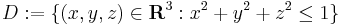$D:=\{(x,y,z)\in\mathbf{R}^3: x^2+y^2+z^2 \leq 1\}$ . Volym av D ges då av uttrycket

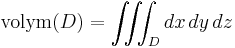$\mathop{\rm volym}(D)=\iiint_D dx\,dy\,dz$ .

Görs ett variabelbyte till sfäriska koordinater enligt

$\left\{\begin{align}x&=r\cos\varphi\sin\theta\\ y&=r \sin\varphi \sin\theta\\ z&=r\cos\theta\end{align}\right.$

transformeras volymelementet dx dy dz till

$dx\,dy\,dz=\left|\frac{d(x,y,z)}{d(r,\theta,\varphi)}\right|\,dr\,d\theta\,d\varphi=r^2 \sin\theta\ dr\,d\theta\,d\varphi$

och området D beskrivs i de nya koordinaterna som

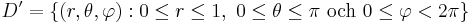$D' = \{(r,\theta,\varphi):0\leq r \leq 1,\ 0\leq \theta \leq \pi\ \text{och}\ 0 \leq \varphi < 2\pi \}$ .

Strikt sett är detta koordinatbyte inte injektivt i hela D, men om vi exkluderar linjen x = y = 0 får vi ett område med samma volym som D där koordinatbytet är injektivt och vi kan tillämpa koordinatbytet i volymintegralen. Volymintegralen blir därför

$\begin{align}\mathop{\rm volym}(D) &= \iiint_{D'} r^2\sin\theta\ dr\,d\theta\,d\varphi\\ &= \int_0 ^{2\pi} d\varphi \int_0 ^\pi \sin\theta\,d\theta \int_0^1 r^2\,dr = 2\pi\cdot 2\cdot \frac{1}{3} = \frac{4\pi}{3}\,\mathrm{.}\end{align}$

Se även

Hessmatris

Jacobimatris

Från Rilpedia

Innehåll

Jakobimatris

Exempel

Jakobideterminanten

Exempel

Användningar

Exempel

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk