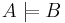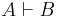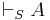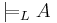Härledningsbegrepp
Från Rilpedia
Härledningsbegrepp är begrepp inom metalogik och bevisteori som används för att beskriva formlers relationer till varandra. Inom logiken finns både semantiska och syntaktiska begepp. Även begreppet implikation inom objektlogiker kan i vissa tillämpningar uppfattas som ett härledningsbegrepp.
Innehåll |
Medför, giltighet
I logik är begreppet medför (en. entails) en relation mellan två uppsättningar formler i ett formellt språk. Om A och B är två uppsättning formler i det formella språket, och om en interpretering som gör alla formler i A sanna gör formlerna/formeln i B sanna/sann, så följer B av A, dvs A medför B. Symboliskt skrivs detta som:
Symbolen kan också utläsas som semantisk giltighet. (Symbolen används även i andra betydelser, bl.a. inom "datavetenskap")
Bevisbar, konsekvens
I logik är begreppet bevisar (en. yields eller proves) en relation mellan två uppsättningar formler i ett formellt system. Om A och B är två uppsättning formler i det formella systemet, och ... så är B bevisbar från A, dvs A bevisar B. Symboliskt skrivs detta som:
Symbolen kan också utläsas som syntaktisk konsekvens. Symbolen introducerades i denna mening av Gottlob Frege [1] 1879.
Fullständighet och sundhet
Ett deduktivt system S är fullständigt eller komplett för språket L om och endast om 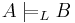 implicerar
implicerar 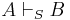 , dvs om alla giltiga argument är deducerbara.
, dvs om alla giltiga argument är deducerbara.
Ett deduktivt system S är sunt för språket L om och endast om 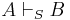 implicerar
implicerar 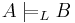 , dvs om inga ogiltiga argument är bevisbara.
, dvs om inga ogiltiga argument är bevisbara.
Begreppet "semantisk giltighet" används olika hos olika författare. Vissa författare avser att en härledning med hjälp av sanningstabeller (dvs mening) skapar semantisk giltighet, andra att det är sanningen hos A och B som avgör semantisk giltighet. Därmed blir begreppen "fullständighet" och "sundhet" också otydliga.
Teorem
En formel A är ett teorem i det formella systemet S om
A är således bevisbar i S men därmed inte nödvändigtvis logiskt sann som kräver att ingen tilldelning till argumenten till S axiom kan göra A falsk (t.ex. om S inte är sunt eller inte komplett).
Tautologi
En formel A är en tautologi i det formella språket L om
A är således giltig i L men därmed inte nödvändigtvis logiskt sann som kräver att ingen tilldelning till argumenten till formlerna i L kan göra A falsk.
Härledbarhet
En formel B är härledbar från en mängd A av satser i det formella systemet S om och endast om det av ett ändligt antal härledningssteg följer att B impliceras av A .
Referenser
- ↑ Gottlob Frege, Begriffsschrift: Eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Halle, 1879.