Johann Peter Gustav Lejeune Dirichlet
Från Rilpedia
 |
|
| Född: | 13 februari 1805 Düren, Franska kejsardömet |
| Död: | 5 maj 1859 Göttingen, Hannover |
| Nationalitet: | Tyskland |
| Forskningsområde: | Matematik |
| Institutioner: | Berlins universitet Breslaus universitet Universität Göttingen |
| Alma mater: | Bonns universitet |
| Akademisk handledare: | Simeon Poisson Joseph Fourier |
| Nämnvärda studenter: | Ferdinand Eisenstein Leopold Kronecker Rudolf Lipschitz Carl Wilhelm Borchardt |
| Känd för: | Dirichlets funktion |
Johann Peter Gustav Lejeune Dirichlet, född 13 februari 1805, död 5 maj 1859, var en tysk matematiker som tillskrivits definitionen av det moderna, allmänna funktionsbegreppet.
Dirichlet och hans släkt härstammade från Richelet i Belgien vilket givit honom hans namn "le jeune de Richelet", dvs "den unge från Richelet". Dirichlet föddes i Düren där hans far var postmästare. Han var gift med Rebecca Mendelssohn, barnbarn till filosofen Moses Mendelssohn och syster till kompositören Felix Mendelssohn-Bartholdy.
Dirichlet blev 1839 professor i matematik i Berlin och 1855 i Göttingen. Han studerade en längre tid i Paris, där Fourier väckte hans intresse för den matematiska fysikens metoder, inom vilket område Dirichlet gjort insatser av stort värde, till en del bestående däri, att han klarare än sina föregångare bestämde villkoren, för metodernas giltighet. Han var även den första som angav lösningen till problemet om en sfärs rörelse i en vätska. Det område, där Dirichlets verksamhet varit av största betydelse, är dock talteori, där han kan sägas vara den förste, som tillämpat analysen på talteorin och därigenom funnit dittills oanade samband mellan skilda grenar av matematiken. Hans första avhandling handlade om Fermats sista sats för vilken han producerade ett delbevis för fallet n = 5 och beviset för n = 14. Dirichlets nya metoder inom talteori har i avseende på epokgörande betydelse jämförts med René Descartes analytiska geometri.
Bland fler av Dirichlets betydande arbeten kan nämnas beviset för förekomsten av oändligt många primtal i varje aritmetisk följd, vars termer inte innehåller någon gemensam faktor, samt bestämningen av antalet klasser av kvadratiska former.
Efter Dirichlets död publicerades han föreläsningar och verk inom talteori av vännen och kollegan Richard Dedekind i Vorlesungen über Zahlentheorie.
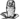Denna artikel är helt eller delvis baserad på material från Nordisk familjebok, 1904–1926 (Not).
