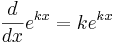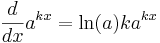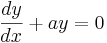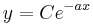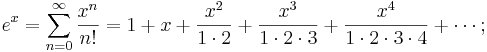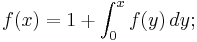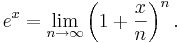Exponentialfunktion
Från Rilpedia
Exponentialfunktionen är en matematisk funktion. Den betecknas
eller
där e är basen i den naturliga logaritmen. För reella x är y alltid positivt, och växer då x växer. Den inversa funktionen är den naturliga logaritmen, vilken är definierad för alla positiva värden.
För rent imaginära tal x är exponentialfunktionen periodisk: Om x = it där t är ett reellt tal och i den imaginära enheten, så gäller att
Innehåll |
Egenskaper
En mer generell exponentialfunktion kan konstrueras genom att sätta
där a > 0 kallas basen. Det är på detta sätt det definieras för komplexa tal, närmare bestämt som
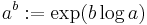 , där log betecknar en lämplig gren av den komplexa (flervärda) logaritmen.
, där log betecknar en lämplig gren av den komplexa (flervärda) logaritmen.
Några räkneregler (gäller för alla 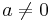 ):
):
Derivator och differentialekvationer
Derivatan av en exponentialfunktion är åter en exponentialfunktion, närmare bestämt
eller allmänt
Detta ger att en differentialekvation av första ordningen
har följande lösning
Detta uttryck används för att beräkna ränta på ränta, radioaktiva ämnens sönderfallshastighet och det ger en approximation av tillväxten av en population då denna är så liten att medlemmarna i populationen inte konkurrerar nämnvärt med varandra om resurser.
Se vidare om differentialekvationer av första ordningen.
Definition
Det finns minst fem olika sätt att definiera exponentialfunktionen som en funktion vars definitionsmängd är de reella talen och vars värdemängd är de positiva reella talen:
- Som en potensserie:
- Som den unika lösningen till följande integralekvation:
- Som talet e upphöjt till talen x;
- Som den inversa funktionen till den naturliga logaritmfunktionen;
- Som en gränsfunktion:
Av dessa kan definitionerna 1 och 5 generaliseras till att gälla mer abstrakta rum är de reella talen. Exempelvis kan man definiera en "exponentialfunktion" i så kallade Banachalgebror; dessa är Banachrum med den extra strukturen att en produkt av två element i Banachrummet förblir ett element i Banachrummet.
Har man väl valt en av ovanstående framställningar som definition av exponentialfunktionen så kommer de övriga fyra att vara teorem om exponentialfunktionens egenskaper.





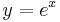
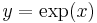
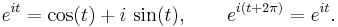
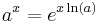
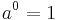
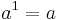
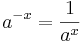
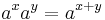
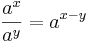
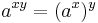
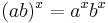
![\ a^{x/n} = \sqrt[n]{a^x}\,\!](/w/images/sv.rilpedia.org/math/a/4/5/a45d9863a53741007ebdb7c00567d7f6.png)