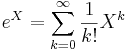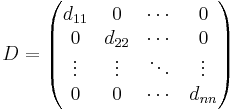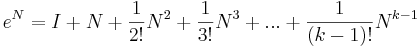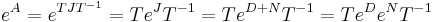Matrisexponentialfunktion

Från Rilpedia

(Omdirigerad från Matrisexponential)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Matrisexponentialfunktionen är inom matematiken en utökning av exponentialfunktionen från komplexa tal till att gälla även kvadratiska matriser, så att man får en matrisfunktion.

Definition

Exponentialfunktionen för matriser definieras genom exponentialfunktionens Maclaurinutveckling:

$e^X = \sum_{k=0}^\infty \frac{1}{k!}X^k$

Denna serie konvergerar för alla matriser, $A .$

Egenskaper

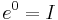$e^0 = I \,$ , för nollmatrisen 0 och enhetsmatrisen I.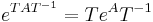
$e^{TAT^{-1}} = T e^A T^{-1}$
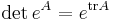
$\det e^A = e^{\operatorname{tr}{A}}$
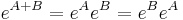$e^{A+B} = e^{A} e^{B} = e^{B} e^{A} \,$ om $A$ och $B$ kommuterar.
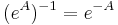$(e^{A})^{-1} = e^{-A} \,$ för alla inverterbara matriser $A$

Beräkning

Diagonalmatriser

Om D är diagonal med diagonelelementen $d i i$ är $e D$ en diagonalmatris med diagonalelementen 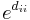$e^{d_{ii}}$ , dvs:

$D = \begin{pmatrix} d_{11} & 0 & \cdots & 0 \\ 0 & d_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & d_{nn} \end{pmatrix}$

$e^D = \begin{pmatrix} e^{d_{11}} & 0 & \cdots & 0 \\ 0 & e^{d_{22}} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & e^{d_{nn}} \end{pmatrix}$

Detta kommer av att en diagonalmatris upphöjt till något tal blir en diagonalmatris med diagonalementen upphöjda till detta tal (vilket inses lätt om man tänker på hur matrismultiplikation funkar). Man kan då betrakta Maclaurinutvecklingen av matrisen varje diagonalelement för sig, vilket per definition blir $e x$ för diagonalelementet x.

Nilpotenta matriser

Om N är en nilpotent matris, dvs $N k = 0$ för något heltal k, definieras $e N$ som:

$e^N = I + N + \frac{1}{2!}N^2 + \frac{1}{3!}N^3 + ... + \frac{1}{(k-1)!}N^{k-1}$

Dvs, Maclaurinutvecklingen av $e X$ tills att det bara blir nollmatriser.

Generalisering

Om matrisen har element som är reella eller komplexa tal kan man använda Jordans normalform för att beräkna $e A$ för alla kvadratiska matriser A. En kvadratisk matris kan då skrivas $A = T J T - 1$ där J är en matris på Jordans normalform. Matrisen J kan skrivas $J = D + N$ för en diagonal matris D och en nilpotent matris N. Så att:

$e^A = e^{TJT^{-1}} = Te^JT^{-1} = Te^{D+N}T^{-1} = Te^De^NT^{-1}$

Se även

Matrisexponentialfunktion

Från Rilpedia

Innehåll

Definition

Egenskaper

Beräkning

Diagonalmatriser

Nilpotenta matriser

Generalisering

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk