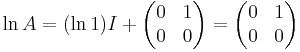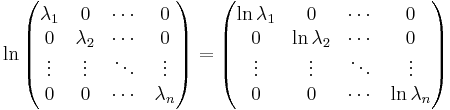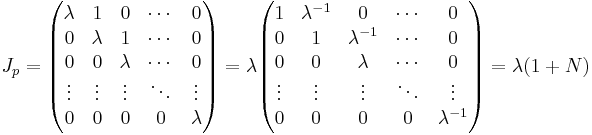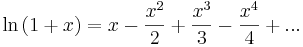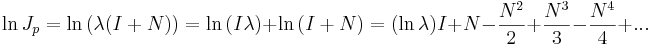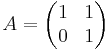Matrislogaritm
Från Rilpedia
Inom matematiken är matrislogaritm en generalisering av begreppet logaritm till att gälla även kvadratiska matriser. Matrislogaritmen är den inversa matrisfunktionen till matrisexponentialen.
Innehåll |
Definition och egenskaper
En matris B är logaritmen till en matris A om A är matrisexponentialen av B:
- eB = A
Matrislogaritmen har följande egenskaper:
- En matris har en logaritm om och endast om den är inverterbar.
- En reell matris kan ha en komplex matris som logaritm.
- Matrislogaritmen är inte unik.
Beräkning
För diagonaliserbara matriser
Om D är en diagonalmatris är logaritmen av D en diagonalmatris med diagonalelement som är logaritmen (för skalärer) av Ds diagonalelement, dvs:
För en diagonaliserbar matris A, dvs A = TDT − 1, gäller att 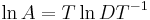 .
.
För ej diagonaliserbara matriser
Alla kvadratiska matriser kan skrivas på Jordans normalform, dvs A = TJT − 1 där J är en blockdiagonal matris där blocken är Jordanblock. Ett Jordanblock Jp kan skrivas som:
Där N är en nilpotent matris med λ − 1 i diagonalen ovanför huvuddiagonalen.
Vi kan nu använda Maclaurinutvecklingen av 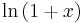 :
:
Så att:
Då N är nilpotent kommer Nk = 0 för något k, så att serien i slutet kommer att konvergera mot en matris.
Exempel
Matrisen:
är ett Jordanblock. Vi får då att: