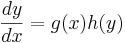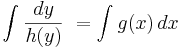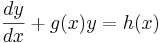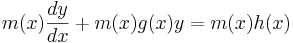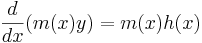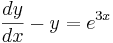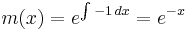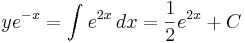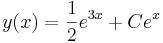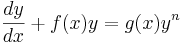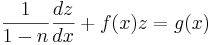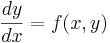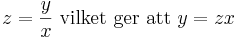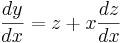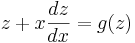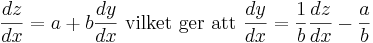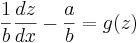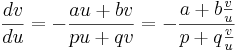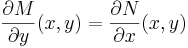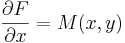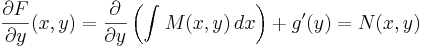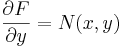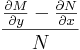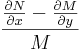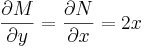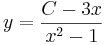Differentialekvationer av första ordningen

Från Rilpedia

Texten från svenska Wikipedia

I differentialekvationer av första ordningen ingår en funktion och funktionens förstaderivata. Det finns flera lösningsmetoder för differentialekvationer av första ordningen, och vilken metod som används beror på av vilken typ differentialekvationen är.

Innehåll

1 Differentialekvationer med separabla variabler
- 1.1 Exempel på differentialekvation med separabla variabler
2 Linjära differentialekvationer
- 2.1 Exempel på linjär differentialekvation
3 Bernoulli-ekvationer
4 Homogena ekvationer
5 Ekvationer där högerledet är en funktion av (ax + by)
6 Ekvationer med linjära koefficienter
7 Exakta ekvationer
- 7.1 Exempel på en exakt differentialekvation
8 Se även

Differentialekvationer med separabla variabler

En ekvation har separabla variabler när den kan skrivas om så att dess respektive variabel, inklusive differential, hamnar på varsin sida om likhetstecknet. Differentialekvationen ska alltså kunna skrivas på formen

$\frac {dy}{dx} = g(x)h(y)$

För att lösa ekvationen multipliceras med $d x$ och divideras med $h (y)$ , och därefter integreras båda leden. Detta ger

$\int_{}^{}\frac {dy}{h(y)}\ = \int_{}^{}g(x)\, dx$

med (den implicita) lösningen

H (y) = G (x) + C

Exempel på differentialekvation med separabla variabler

Exemplet visar hur en differentialekvation med separabla variabler löses.

$\frac {dy}{dx} = y(2 + \sin x)$

Multiplicera båda leden med $d x$ , dividera med $y$ och integrera:

$\int_{}^{}\frac {dy}{y}\ = \int_{}^{}(2 + \sin x)\, dx$

ln y + C 1 = 2 x - cos x + C 2

De båda konstanterna kan lika gärna skrivas som en konstant $C$ , och därefter löses $y$ ut:

ln y = 2 x - cos x + C

y = e 2 x - cos x + C = C e 2 x - cos x

Linjära differentialekvationer

En linjär differentialekvation av första ordningen kan skrivas på följande form, som kallas standardform:

$\frac {dy}{dx} + g(x)y = h(x)$

För att lösa denna ekvation bestäms en funktion $m (x)$ , som är sådan att om ekvationen multipliceras med denna, så blir vänsterledet derivatan av produkten $m (x) y$ . Funktionen $m (x)$ kallas integrerande faktor, och bestäms genom

$m(x) = e^{\int_{}^{}g(x)\, dx}$

Multiplicera båda leden i ekvationen med $m (x)$

$m(x) \frac {dy}{dx} + m(x)g(x)y = m(x)h(x)$

Vänsterledet är nu derivatan av produkten $m (x) y$

$\frac {d}{dx}(m(x)y) = m(x)h(x)$

och lösningen på differentialekvationen är

$y(x) = \frac {1}{m(x)}(\int_{}^{}m(x)h(x)\, dx + C)$

Exempel på linjär differentialekvation

Exemplet visar hur man löser den linjära differentialekvationen

$\frac {dy}{dx} - y = e^{3x}$

Beräkna den integrerande faktorn. Integrationskonstanten utelämnas, eftersom man senare integrerar en gång till, och får en ny konstant.

$m(x) = e^{\int_{}^{}-1\, dx} = e^{-x}$

Multiplicera differentialekvationen med den integrerande faktorn:

$e^{-x} \frac {dy}{dx} - ye^{-x} = e^{-x}e^{3x}$

vilket förenklas till

$\frac {d}{dx}(ye^{-x}) = e^{2x}$

Integrera båda leden och lös därefter ut $y$

$ye^{-x} = \int_{}^{}e^{2x}\, dx = {1 \over 2}e^{2x} + C$

$y(x) = {1 \over 2}e^{3x} + Ce^x$

Bernoulli-ekvationer

En Bernoulli-ekvation kan skrivas på formen

$\frac {dy}{dx} + f(x)y = g(x)y^n$

Om $n$ är 0 eller 1 är ekvationen linjär, se Linjära differentialekvationer ovan, i annat fall löses den på följande sätt:

Dividera först med $y n$ vilket ger

$y^{-n}\frac {dy}{dx} + f(x)y^{1 - n} = g(x)$

Gör substitutionen

z = y 1 - n

och derivera $z$ med avseende på $x$ , med resultatet

$\frac {dz}{dx} = (1-n)y^{-n} \frac {dy}{dx}$

Ersätt $y$ med $z$ i differentialekvationen

$\frac {1}{1-n} \frac {dz}{dx} + f(x)z = g(x)$

Denna ekvation är linjär och löses som i avsnittet Linjära differentialekvationer ovan, varefter man åter ersätter

z = y 1 - n

för att få resultatet som en funktion i $y$ .

Homogena ekvationer

Om högra ledet i följande differentialekvation kan uttryckas som en funktion i förhållandet $y / x$ , kallas ekvationen homogen.

$\frac {dy}{dx} = f(x, y)$

För att lösa en homogen ekvation görs substitutionen

$z = {y \over x} \mbox { vilket ger att } y = zx$

Derivera $y$ med avseende på $x$ :

$\frac {dy}{dx} = z + x\frac {dz}{dx}$

Sätt in i den ursprungliga ekvationen

$z + x\frac {dz}{dx} = g(z)$

Denna differentialekvation är nu en differentialekvation med separabla variabler och löses som i avsnittet ovan som behandlar sådana. Slutligen ersätter man $z$ med $y / x$ för att få svaret i de ursprungliga variablerna.

Ekvationer där högerledet är en funktion av (ax + by)

I ekvationer av denna form gör man substitutionen

z = a x + b y

som ger att

$\frac {dz}{dx} = a + b\frac {dy}{dx} \mbox { vilket ger att } \frac {dy}{dx} = {1 \over b}\frac {dz}{dx} - {a \over b}$

Sätt in i den ursprungliga ekvationen

${1 \over b}\frac {dz}{dx} - {a \over b} = g(z)$

vilket är en differentialekvation med separabla variabler och löses som i avsnittet ovan som behandlar sådana. Slutligen ersätter man $z$ med $a x + b y$ för att få svaret i de ursprungliga variablerna.

Ekvationer med linjära koefficienter

Ekvationer med linjära koefficienter är av formen

(a x + b y + c) d x + (p x + q y + r) d y = 0

Om $a q = b p$ är ekvationen av formen dy/dx = f(ax + by) och löses som i avsnittet ovan som behandlar sådana. Om $c = r = 0$ är ekvationen homogen och löses som i avsnittet Homogena ekvationer. I andra fall gör man följande substitutioner

x = u + h och y = v + k

Där $h$ och $k$ är konstanter som fås fram genom att lösa ekvationssystemet

a h + b k + c = 0

p h + q k + r = 0

De nya variablerna insatta i differentialekvationen ger den homogena ekvationen

$\frac {dv}{du} = -\frac {au + bv}{pu + qv} = -\frac {a + b {v \over u}}{p + q {v \over u}}$

som löses som i avsnittet Homogena ekvationer.

Exakta ekvationer

Alla differentialekvationer av första ordningen kan skrivas på formen

M (x, y) d x + N (x, y) d y = 0

Denna ekvation sägs vara exakt om

$\frac {\partial M}{\partial y}(x, y) = \frac {\partial N}{\partial x}(x, y)$

Då är

$\frac {\partial F}{\partial x} = M(x, y)$

Denna ekvation integreras med avseende på $x$ vilket ger

$F(x, y) = \int_{}^{} M(x, y)\, dx + g(y)$

som deriveras med avseende på $y$ vilket ger

$\frac {\partial F}{\partial y}(x, y) = \frac {\partial}{\partial y} \left(\int_{}^{} M(x, y)\, dx \right) + g'(y) = N(x, y)$

Ur denna funktion löses $g'(y)$ som därefter integreras för att få $g (y)$ . (Vid denna integration sätts integrationskonstanten till 0, eftersom den ingår i den implicita lösningen.) Därmed är $F (x, y)$ klar, och den implicita lösningen till differentialekvationen är

F (x, y) = C

Man kan lika gärna börja med

$\frac {\partial F}{\partial y} = N(x, y)$

och integrera med avseende på $y$ . Man väljer $M$ eller $N$ beroende på vilken som är lättast att integrera.

Om differentialekvationen inte är exakt, kan man i vissa fall multiplicera med en integrerande faktor $m (x, y)$ , som gör ekvationen exakt.

Om

$\frac {\frac {\partial M}{\partial y} - \frac {\partial N}{\partial x}} {N}$

bara beror av $x$ är den integrerande faktorn $e$ upphöjt till integralen med avseende på $x$ av detta uttryck.

Om

$\frac {\frac {\partial N}{\partial x} - \frac {\partial M}{\partial y}} {M}$

bara beror av $y$ är den integrerande faktorn $e$ upphöjt till integralen med avseende på $y$ av detta uttryck.

Exempel på en exakt differentialekvation

Här löses differentialekvationen

(2 x y + 3) d x + (x 2 - 1) d y = 0

Först testas om ekvationen är exakt. Här är

M (x, y) = 2 x y + 3 och N (x, y) = x 2 - 1

vilket ger

$\frac {\partial M}{\partial y} = \frac {\partial N}{\partial x} = 2x$

Alltså är differentialekvationen exakt.

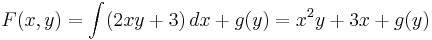
$F(x, y) = \int_{}^{} (2xy + 3)\, dx + g(y) = x^{2}y + 3x + g(y)$

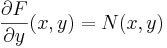
$\frac {\partial F}{\partial y}(x, y) = N(x, y)$

x 2 + g'(y) = x 2 - 1

Alltså är

g'(y) = - 1

Detta integreras (och integrationskonstanten sätts till 0):

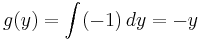
$g(y) = \int_{}^{}(-1)\, dy = -y$

F (x, y) = x 2 y + 3 x - y

och den implicita lösningen är

x 2 y + 3 x - y = C

Just i detta fallet kan man lösa ut $y$ och få den explicita lösningen

$y = \frac {C - 3x}{x^{2} - 1}$

Se även

Differentialekvation