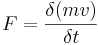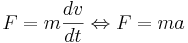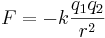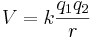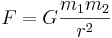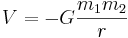Kraft
Från Rilpedia
- För andra betydelser, se Kraft (olika betydelser).
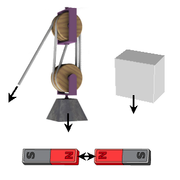
Begreppet kraft är en abstraktion inom fysiken för att förklara och beskriva orsaken till förändringar i ett systems rörelse. Kraftbegreppet infördes i dagens formulering av Isaac Newton. Inom den klassiska fysiken förklarar Newtons tre rörelselagar kroppars rörelse under inverkan av krafter, dessa tre lagar kan sägas definiera krafter som verkar på ett system. De tre lagarna är:
- Ett föremål fortsätter att vara i vila, eller fortsätter sin rörelse i samma riktning och med samma konstanta hastighet som förut, såvida ingen kraft förändrar detta tillstånd.
- Om en kraft F verkar på ett föremål så gäller att
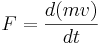 , där mv är rörelsemängden och t är tiden.
, där mv är rörelsemängden och t är tiden. - Om ett föremål utövar en kraft på ett annat föremål, så kommer det andra föremålet utöva en kraft på det första, som till storleken är lika stor, men riktad åt motsatt håll.
Innehåll |
Enhet
Enheten för kraft är newton (N). 1 newton definieras som den kraft som krävs för att ge en massa på 1 kg en acceleration på 1 meter/sekund². Äldre enheter är kilopond och dyn.
Definitioner
En kraft är en fysikalisk storhet med en storlek och en riktning. Krafter som verkar på ett objekt kan sålunda representeras med vektorer och adderas (med vektoralgebra) till en nettokraft. Om nettokraften är skiljd från noll förändras objektets rörelsevektor, det vill säga dess fart eller rörelseriktning (eller båda delarna).
Enligt Newtons andra lag definieras en kraft genom förändringen av ett systems rörelsemängd över tiden.
Där δ anger en förändring av storhetena mv (rörelsemängden, systemets massa gånger hastighet) och t (tiden). Då tidsdifferensen görs allt mindre, erhålls i gränsövergången då δt går mot noll den momentana kraften som verkar på systemet.
Kraften definieras då som tidsderivatan av rörelsemängden. Inom klassisk dynamik är ofta systemets massa konstant under tiden kraften verkar och då förenklas Newtons andra lag till:
Där a är systemets acceleration och m är systemets massa.
Referenssystem där Newtons andra lag på formen 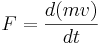 gäller kallas intertialsystem och innebär att systemet i sig inte accelererar. Denna idealisering passade in i dåtidens naturfilosofiska tro på ett absolut rum och en absolut tid. Ett äkta intertialsystem finns i egentlig mening inte, men för praktiska ändamål kan man ändå i de flesta fall hitta ett referenssystem som är en god approximation till ett intertialsystem. I vissa fall är referenssystemet jorden en tillräckligt god approximation av ett intertialsystem, men om man studerar planetsystemet kan man till exempel välja ett referenssystem som fixeras i avlägsna stjärnor och galaxer. Tron på ett absolut rum ledde vetenskapsmännen att söka efter detta i och med fastställandet av ljusets hastighet i Maxwells ekvationer, se vidare etern.
gäller kallas intertialsystem och innebär att systemet i sig inte accelererar. Denna idealisering passade in i dåtidens naturfilosofiska tro på ett absolut rum och en absolut tid. Ett äkta intertialsystem finns i egentlig mening inte, men för praktiska ändamål kan man ändå i de flesta fall hitta ett referenssystem som är en god approximation till ett intertialsystem. I vissa fall är referenssystemet jorden en tillräckligt god approximation av ett intertialsystem, men om man studerar planetsystemet kan man till exempel välja ett referenssystem som fixeras i avlägsna stjärnor och galaxer. Tron på ett absolut rum ledde vetenskapsmännen att söka efter detta i och med fastställandet av ljusets hastighet i Maxwells ekvationer, se vidare etern.
Exempel på olika krafter
De fyra fundamentala naturkrafterna
Se vidare Fundamental växelverkan
Konservativa krafter
Dissipativa krafter
Fiktiva krafter
Krafter och potentialer
Den matematiska formuleringen av kraftbegreppet är starkt kopplat till det beskrivna systemets totala energi. I den enklaste formen är ett systems totala energi summan av den potentiella och den kinetiska energin hos systemet. Den potentiella energin kopplas till den kraft som systemet påverkas av, till exempel en elektrisk kraft som verkar på en elektrisk laddning i ett elektriskt fält.
Den elektriska Coulombkraften mellan två laddade partiklar q1 och q2 på avståndet r från varandra skrivs som:
Detta kan omskrivas till en elektrisk potential upplevd av q1 givet av laddningen q2
Likaledes kan den gravitationella kraften mellan två massor m1 och m2 på avståndet r från varandra skrivs som:
Detta kan omskrivas till en gravitationell potential upplevd av m1 givet av massan m2
Historik
Aristoteles ansåg att en kraft (han använde dock inte detta uttryck) behövdes för att hålla en kropp i rörelse. Sålunda går Newtons och Aristoteles syn på rörelse stick i stäv mot varandra. Med Newtons definition krävs en kraft för att förändra en kropps rörelse. En kropp i absolut vakuum och långt från annan materia skulle sålunda bete sig helt olika enligt dessa två förklaringar. Vidare hävdade Aristoteles även att olika tunga föremål faller olika fort.
Galileo Galilei utförde experiment för att studera fallande kroppar och tog genom sina studier första steget mot en omvälvning av den förhärskande bilden av hur kroppar påverkas av krafter, bland annat hävdade han att tunga och lätta föremål faller lika fort, något som han enligt en välkänd myt ska ha demonstrerat genom att släppa olika tunga föremål från lutande tornet i Pisa.
Den danske naturfilosofen Tycho Brahe utförde noggranna studier på himlakroppar och noterade deras rörelser i tabeller. Under sin tid som hovastronom mötte Brahe den matematiskt begåvade Johannes Kepler. Kepler systematiserade Brahes tabeller och fann att himlakropparna följde vissa mönster. Han härledde ur Brahes tabeller Keplers rörelselagar för himlakropparna. Slutsatsen av Keplers arbeten var att himlakropparna rörde sig i ellipser med solen i ena brännpunkten. Newtons arbete under slutet av 1600-talet förklarade Keplers lagar, varför olika tunga föremål faller lika fort och mycket annat. För första gången gavs en enhetlig teori för kroppars rörelse. Genom Newtons arbete sammanbands den celesta mekaniken med mer närliggande mekanik (lutande plan, fallande kroppar). Newton ledde sålunda en revolution genom att hävda att samma principer styr experiment utförda på jorden och himlakropparnas rörelser. Under 1700- och 1800-talen utarbetades olika förfiningar av Newtons terorier. Värt att nämna är d'Alemberts princip, Langranges arbeten och slutligen Hamiltons formulering av lagen om minimal verkan. Genom dessa senare arbeten gavs mekaniken och kraftbegreppet en konsistent förklaring och kraftfulla metoder för problemlösning och teoribyggande sattes på plats. Viktiga bidrag rörande kraftbegreppet och tillhörande teorier gavs också av bland annat Euler, Bernoullie och Laplace.
I och med Maxwells formulering av lagarna för elektromagnetism framkom att ljusets hastighet i vakuum intar en särställning inom fysiken. Under de senare decennierna av 1800-talet arbetades intensivt med att förklara ljusets hastighet inom ramen för den Newtonska mekaniken och Maxwells elektrodynamik. Detta arbete byggde på existensen av idén om det absoluta rummet och den absoluta tiden, såsom postulerats i den newtonska mekaniken. Michelson och Morley genomförde ett berömt experiment för att påvisa ljusets hastighet genom etern, dock utan framgång. Slutligen löstes denna fråga av Albert Einstein som postulerade vad ingen annan fysiken vågat - Newton hade fel om det absoluta rummet och den absoluta tiden. Einsteins arbete, som resulterade i den speciella och den allmänna relativitetsteorin, kullkastade Newtons principer och gav en ny förklaring på den celesta mekaniken. Himlakroppar hålls i sina banor kring varandra på grund av en materiaansamlings krökning av den s.k. rumtiden.
Decennierna efter Einsteins arbete utvecklade också kvantmekaniken och förklarade den diskrepans mellan teori och experiment vad gäller mycket små fysikaliska system (svartkroppsstrålning, atomära spektra, mm). Enligt denna teori förklaras kraftbegreppet som ett utbyte av kraftförmedlande partiklar, till exempel fotonen för elektromagnetiska krafter.
Idag råder ett febrilt arbete för att söka hitta en teori som förklarar diskrepansen mellan kvantmekanik och den allmänna relativitetsteorin. Se till exempel loopkvantgravitation och strängteori.
Relaterade storheter
Kraft används för att direkt härleda energi och tryck. Energi omsätts om kraften får verka i en viss sträcka, energimängden blir då proportionell mot kraften och mot sträckan. Tryck är kraft per ytenhet, och har till skillnad från kraft påtaglig effekt på vardagslivet. Elefanterna måste ha stora fötter för att inte trampa igenom jorden. I vardagligt tal förekommer uttryck som "elektrisk kraft", och det är vanligtvis ett felaktigt uttryck. Man brukar mena elektrisk effekt eller möjligen elektrisk energi. Våra tankar förleds också av den vardagliga erfarenheten av handkraft; vi blir trötta av att hålla ett tungt föremål. Vi överför ingen energi till det föremål vi håller, men våra kroppsfunktioner omsätter ändå mer energi än vanligt, som avgår som spillvärme.
|
|||||||||||