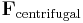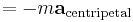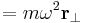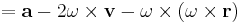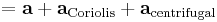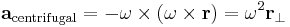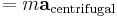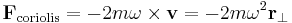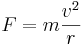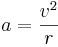Centrifugalkraft
Från Rilpedia
Centrifugalkraft (från latinets centrum och fugere (undflyende)) är en term vilken kan referera till två olika krafter vilka är relaterade till rotation. Båda är riktade ifrån rotationscentrum men de objekt vilka de verkar på är olika.
- En reell eller "reaktiv" centrifugalkraft uppträder som en reaktion på en centripetal acceleration som verkar på en massa. Denna centrifugala kraft är till storleken lika med den centripetala kraften men riktad från rotationscentrum och verkar på det objekt vilket orsakar den centripetala accelerationen. Trots att centripetalkraften i denna betydelse användes av Isaac Newton används termen sällan i moderna diskussioner.
- En pseudo eller "fiktiv" centrifugalkraft uppträder när en roterande referensram används for analys. Accelerationen (den sanna) av referensramen ersätts med en (fiktiv) centrifugalkraft som påverkar alla objekt och är riktad från rotationscentrum.
Båda typerna av krafter kan åskådliggöras med en passagerare som färdas i en bil. Om bilen färdas genom en kurva förefaller passageraren röra sig mot bilens yttre sida och sedan tryckas mot dörren. I en referensram som roterar med samma hastighet som bilen i sin kurva (en modell som faller sig naturlig för den som färdas med bilen) förefaller det som om en kraft trycker passageraren bort från rotationscentrum. Detta är en fiktiv kraft, inte en kraft som utövas av något annat objekt. Illusionen uppkommer när bilen är referensram genom att denna ignorerar bilens acceleration (som härrör från bilens riktningsändring).
Emellertid, den kraft med vilken passageraren pressas mot dörren är verklig. Denna kraft kallas reaktiv kraft därför att den beror på en "passiv" växelverkan med bilen (som accelererar och därigenom utövar en kraft, är "aktiv") och då denna kraft är riktad från rotationscentrum är den en centrifugalkraft. Observera att denna kraft inte uppkommer förrän passgeraren får kontakt med dörren. Bilen utövar en motriktad centripetal kraft riktad mot rotationscentrum vars storlek är den samma som den centrifugala kraftens storlek.
Innehåll |
Reaktiv centrifugalkraft
Sedda från ett inertialsystem är tillämpningarna av Newtons rörelselagar enkla. Passagerarens tröghetskraft motstår accelerationen, och får passageraren att röra sig med konstant hastighet och riktning när bilen börjar att svänga. Från denna synpunkt rör sig inte passageraren mot banans "utsida" vilken bilen följer; istället kröker sig bilens bana och möter passageraren.
När bilen får kontakt med passageraren påverkar bilen denne med en sidledes verkande kraft och accelererar passageraren i takt med bilens acceleration. Denna kraft kallas centripetal ("centrumsökande") kraft då dess associerade riktningsvektor ändrar riktning för att svara mot en annan punkt i den cirkulära banan.
Om bilen verkar med en kraft på passageraren så måste passageraren verka på bilen med en lika stor men motriktad kraft. Då den är motriktad är denna reaktiva kraft riktad bort från centrum. Det är viktigt att notera att denna centrifugala kraft verkar på bilen, inte på passageraren.
Den centrifugala reaktionskraft med vilken passageraren trycker mot dörren ges av
där 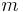 är massan av det roterande objektet.
är massan av det roterande objektet.
Fiktiv centrifugalkraft
Inom den klassiska fysiken används intertialsystem som referens för mekanikens lagar och vid analys. Vid användande av ett roterande referenssystem överförs fysikens lagar från det mest bekväma inertialsystemet till det roterande referenssystemet. Med antagande av en konstant rotationshastighet åstadkoms detta genom att två koordinataccelerationer adderas vilka korrigerar för koordinataxlarnas rotation:
där 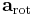 är accelerationen relativt det roterande referenssytemet,
är accelerationen relativt det roterande referenssytemet, 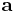 är accelerationen relativt inertialsystemet,
är accelerationen relativt inertialsystemet, 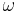 är vinkelhastighetens vektor vilken beskriver referenssystemets rotation,
är vinkelhastighetens vektor vilken beskriver referenssystemets rotation, 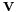 är objektets hastighet relativt det roterande referenssystemet, och
är objektets hastighet relativt det roterande referenssystemet, och 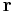 är en vektor från en godtycklig punkt på rotationsaxeln till objektet.
är en vektor från en godtycklig punkt på rotationsaxeln till objektet.
Den sista termen är den centrifugala accelerationen och vi har:
där 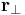 är komponenten av
är komponenten av 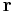 vinkelrät mot rotationsaxeln.
vinkelrät mot rotationsaxeln.
Ett alternativt sätt att hantera en roterande referensram är att göra Newtons rörelselagar articifiellt valida genom att addera pseudokrafter och se dessa som orsak till ovanstående accelerationstermer. Den centrifugala accelerationen adderas till varje objekt och anses betingad av den centripetala kraften given av
där 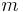 är objektets massa.
är objektets massa.
Denna pseudo- eller fiktiva centrifugala kraft är en tillräcklig korrektion till Newtons andra lag endast om objektet är stationärt i den roterande referensramen. Objekt som rör sig med avseende på den roterande referensramen måste associeras med en andra pseudokraft, Corioliskraften:
En kropp som är stationär med avseende på den icke-roterande referensramen kommer att ses rotera när den observeras från den roterande referensramen. Den centripetala kraften 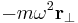 som krävs för att förklara denna observerade rotation är summan av den centrifugala pseudokraften
som krävs för att förklara denna observerade rotation är summan av den centrifugala pseudokraften 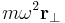 och Corioliskraften (
och Corioliskraften (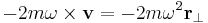 ). Då denna centripetala kraft enbart består av bidrag från pseudokrafter finns ingen motsvarande reaktiv kraft.
). Då denna centripetala kraft enbart består av bidrag från pseudokrafter finns ingen motsvarande reaktiv kraft.
Övrigt
Centrifugalkraftens belopp kan tecknas
där F är kraftens storlek i newton, m är objektets massan i kilogram, r är radien i meter och v är objektets hastighet i banan = m2πrf där f är rotationsfrekvensen i Hz.
Vi ser av uttrycket att centrifugalaccelerationens belopp är