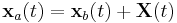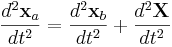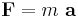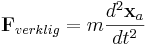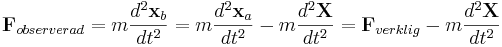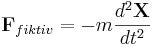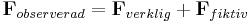Fiktiv kraft

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

En fiktiv kraft, även kallad pseudokraft, är en kraft som verkar på alla massor i ett icke-inertialsystem, till exempel en roterande referensram. Kraften uppstår inte genom fysikalisk växelverkan utan från den icke-inertiala referensramens egen acceleration. Enligt Newtons andra lag F = ma, är fiktiva krafter alltid proportionella mot massan m på vilken krafterna verkar.

Generell härledning

Betrakta en partikel med massan m och positionvektorn xa(t) i ett specifikt inertialsystem A. Antag en icke-inertial referensram B vars position relativt inertialsystemet är givet av X(t). Då B är icke-inertialt existerar d2X/dt2 (accelerationen av referensram B med avseende på referensram A är skilt från noll). Låt partikelns position i referensram B vara xb(t). Då har vi

\bold{x}_a(t) = \bold{x}_b(t) + \bold{X}(t)

Om uttrycket deriveras två gånger med avseende på tiden erhålls

\frac{d^2\bold{x}_{a}}{dt^2} = \frac{d^2\bold{x}_{b}}{dt^2} + \frac{d^2\bold{X}}{dt^2}

Betrakta nu kraften. Enligt Newtons andra lag är

\bold{F} = m\ \bold{a}

Den verkliga kraften är kraften i referensram A (inertialsystemet), så

\bold{F}_{{verklig}} = m \frac{d^2\bold{x}_{a}}{dt^2}

Antag att vi försöker lösa ett problem i referensram B. Det kan vara nyttigt att betrakta den observerade kraften i denna refernsram, vilken ges av

\bold{F}_{{observerad}} = m \frac{d^2\bold{x}_{b}}{dt^2} = m \frac{d^2\bold{x}_{a}}{dt^2} - m \frac{d^2\bold{X}}{dt^2} = \bold{F}_{{verklig}} - m \frac{d^2\bold{X}}{dt^2}

Låt oss nu definiera en systempunktskraft

\bold{F}_{{fiktiv}} = - m \frac{d^2\bold{X}}{dt^2}

vilket sluligen ger

\bold{F}_{{observerad}} = \bold{F}_{{verklig}} + \bold{F}_{{fiktiv}}

Det går således att lösa problem i referensramen B genom att anta att Newton's andra lag gäller (med avseende på kvantiteterna i referensram B) om Ffiktiv behandlas som en tillagd "verklig" kraft.

Gravitationen som en fiktiv kraft

Alla fiktiva krafter är proportionella mot massan av det objekt på vilket de verkar, vilket också är sant för gravitationen. Detta ledde Albert Einstein till att förmoda att också gravitationskraften är en fiktiv kraft. Han noterade att en observatör i fritt fall i en sluten låda var oförmögen att registrera gravitationskraften; fritt fallande referensramar är ekvivalenta med ett inertialsystem (ekvivalensprincipen). Einstein kunde så småningom visa att gravitationskraften verkligen är en fiktiv kraft. Den observerade accelerationen är i själva verket en inertial rörelse i en krökt rumtid. Detta är den essentiella fysiken i Albert Einsteins allmänna relativitetsteori.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Fiktiv_kraft"
Personliga verktyg