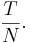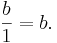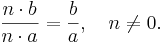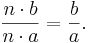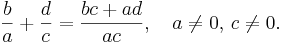Från Rilpedia

Rationella tal, inom matematiken, är en benämning på sådana tal som kan skrivas som en kvot (ett bråk) av två heltal:

I vardagligt språk kallas ett sådant tal för bråktal och heltalet T är bråkets täljare och heltalet N bråkets nämnare.

Tillsammans utgör de rationella talen en mängd som vanligtvis betecknas med bokstaven Q. Ett alternativt sätt att uppfatta denna mängd är som mängden bestående av alla lösningar (x) till ekvationer a x - b = 0, där b är ett heltal och a är ett heltal som inte är lika med talet noll.

Några räkneregler

Om vi uppfattar elementen i mängden Q som lösningar till ekvationer ax - b = 0, så kan vi härleda räkneregler för bråktal.

• 

Bråket b/1 löser ekvationen 1x-b = 0, det vill säga x = b. Eftersom ekvationen endast har en lösning, så måste talen b/1 och b vara lika, det vill säga b/1=b.

• 

Låt n vara ett heltal, som inte är lika med talet noll. Bråket (nb)/(na) är en lösning till ekvationen (na)x-(nb)=0. Genom att bryta ut den gemensamma faktorn n, kan vi omforma ekvationen till n(ax - b) = 0. Den enda möjligheten för denna ekvation att vara sann är om ax-b=0, eftersom vi vet att heltalet n inte är lika med noll. Men detta innebär att talet x – som ju var bråket (nb)/(na) – är lika med bråket b/a:

• 

Vi börjar med att notera att bråket b/a är en lösning till ekvationen ax-b=0, och att bråket d/c är en lösning till ekvationen cy-d=0. Vi skall visa att talet x+y är en lösning till ekvationen (ac)z-(bc+ad)=0, eftersom denna ekvation har en lösning som är bråket (bc+ad)/(ac).

För att göra detta multiplicerar vi x-ekvationen med heltalet c och y-ekvationen med heltalet a och adderar de två erhållna ekvationerna: (acx-bc)+(acy-ad)=0. Denna nya ekvation omformar vi genom att bryta ut den gemensamma faktorn ac, vilket ger oss den sökta ekvationen: ac(x+y)-(bc+ad)=0.

Några egenskaper

• Sedd som en delmängd av de reella talen utgör de rationella talen en så kallad tät mängd; Detta innebär att det alltid finns ett annat rationellt tal mellan två rationella tal, och att varje reellt tal kan approximeras godtyckligt väl med ett rationellt tal.

• Man kan visa att den bästa approximationen av ett reellt tal med ett rationellt tal fås med så kallade kedjebråk, av vilket följande är ett exempel:

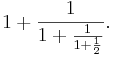
Ändliga kedjebråk – av vilka ovanstående är ett exempel – motsvarar rationella tal, och oändliga kedjebråk motsvarar så kallade irrationella tal.

• De rationella talen utgör vad som kallas en uppräknelig mängd, vilket innebär att det i viss mening finns lika många rationella tal som det finns heltal. Detta kan tyckas vara motsägelsefullt, eftersom mängden av alla heltal är en äkta delmängd av Q; Detta följer av den första räkneregeln för bråktal som vi härledde ovan: b/1 = b där b är ett heltal.

• Det faktum att kardinaltalet för Q är lika med kardinaltalet för Z (mängden av alla heltal), gör att man kan koppla samman varje rationellt tal med ett unikt heltal, och vice versa; På 'matematiska' säger man att det existerar en bijektiv avbildning mellan mängderna Q och Z.

Se även

• Irrationella tal
• Reella tal
• Kardinaltal
• Heltal
• Kedjebråk
• Kroppsutvidgning
• Talkropp
• Galoisteori

Olika typer av matematiska tal

Naturliga tal - Heltal - Positiva tal - Noll - Negativa tal - Rationella tal - Irrationella tal - Reella tal - Algebraiska tal - Transcendent tal - Imaginära tal - Komplexa tal - Hyperkomplexa tal (Kvaternioner Oktonioner Sedenioner) - Perfekta tal