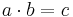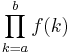Produkt (matematik)

Från Rilpedia

(Omdirigerad från ∏)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Produkt eller faktum är resultatet av multiplikation.

Innehåll

Produkt av tal

Resultat av en multiplikation

Resultatet av en multiplikation kallas produkt. I uttrycket

a \cdot b=c

kallas a och b faktorer medan c kallas produkt.

Produkttecken

Om ett större antal faktorer ska multipliceras ihop, kan produkten ibland skrivas förkortat.

\prod_{k=a}^b f(k)

betyder produkten av alla faktorer f(k) där k varierar från a till b. Tecknet ∏ är den grekiska bokstaven pi och kallas här produkttecken. Produktnotationen är särskilt användbar beträffande produkter med oändligt eller okänt antal faktorer.

Som exempel kan produkten

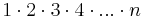1 \cdot 2 \cdot 3 \cdot 4 \cdot ... \cdot n,

det vill säga n-fakultet, skrivas

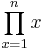\prod_{x=1}^n x.

Se även

Produkt av vektorer

Vektorer kan multipliceras till skalärprodukter och vektorprodukter. I funktionalanalys talar man om inre produkt och yttre produkt.

Cartesisk produkt

Huvudartikel: Cartesisk produkt

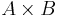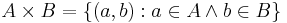Produkten (även kallad den cartesiska produkten) av två mängder A och B är mängden av alla ordnade par (a, b) vars första element a finns i A och vars andra element b finns i B. Produkten av A och B skrivs A \times B, så definitionen kan sammanfattas A \times B = \{ (a,b) : a \in A \and b \in B\}.

Man kan också bilda cartesiska produkter av ett större antal mängder. Produkten A × B × C av de tre mängderna A, B och C består av alla trippler (a,b,c), där a ∈ A, b ∈ B och c ∈ C. Allmänt gäller att om (Mi)i∈I är en familj av mängder över en indexmängd av godtycklig storlek, så definieras den cartesiska produkten av denna familj genom

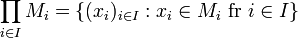\prod_{i\in I} M_i = \{ (x_i)_{i\in I} : x_i \in M_i \hbox{ för } i\in I\}.

När indexmängden består av de n första positiva heltalen, alltså I = { 1, 2, ..., n}, så skrivs produkten hellre som

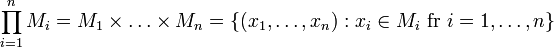\prod_{i=1}^n M_i = M_1 \times \ldots \times M_n = \{ (x_1,\ldots,x_n) : x_i \in M_i \hbox{ för } i = 1,\ldots,n \}.

Formellt sett torde till exempel A × B × C, (A × B) × C och A × (B × C) vara olika mängder, eftersom oftast (a,b,c), ((a,b),c) och (a,(b,c)) definieras på ett sådant sätt att de är olika. I praktiken benandlar man dock i allmänhet dessa som samma mängd genom att man identifierar trippeln och de två "blandade" paren.

Produkten A × A kan också skrivas A2, A × A × A skrivs också A3, ock så vidare. En vanlig tillämpning är beteckningen för reella talplanet, 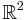\mathbb{R}^2 eller R2.

Exempel:

  • {a, b, c} × {d, e} = {(a, d), (a, e), (b, d), (b, e), (c, d), (c, e)}

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Produkt_(matematik)"
Personliga verktyg