Division (matematik)

Från Rilpedia

(Omdirigerad från ÷)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Division utgör en av de traditionella operatorerna inom aritmetiken och man skulle kunna säga att den precis som subtraktion är en form av minskning av ett tal.

Illustration av 20/4=5

Subtraktion mellan två tal ger en differens och divsion ger en kvot. Skillnaden i dessa operationer ligger i differensen och kvoten.

Differensen mellan två tal a och b skrivs som a-b, där differensen utgör talet a minskat med b. Om a=20 och b=4 kommer alltså differensen vara 16.

Kvoten mellan a och b skrivs ofta som a/b, där kvoten utgör talet a uppdelat i b antal delar. Precis som i tidigare fall där a=20 och b=4 så är då kvoten 5.

En lite tydligare förklaring av detta kan ses i bilden till höger som väldigt bra illustrerar 20 uppdelat i 4 lika stora delar. Talet 5 räknas förövrigt i detta fall som ett rationellt tal.

Talet a minskar alltså vid både division och subraktion men det sker på olika sätt.

Precis som man kan säga att subraktion är additionens motsats så utgör divisionen motsatsen till multiplikationen.

I en division a/b får talet b inte vara 0 då detta är omöjligt eftersom oändligheten inte är ett tal och man låter därför detta vara odefinierat. Mer om detta kan läsas i division med noll.

Innehåll

Historia

Exakt när divisionen uppkom är inte helt klart. Man vet dock att den användes långt före den fick sin matematiska definition. Det var framförallt när talrepresentationen som man har idag tog form som aritmetiken och dess operatorer utvecklades till vad det är idag. När bråk infördes gjordes det möjligt att verkligen fullt ut definiera divisionen.

Det har under människans historia funnits en mängd stora civilisationer och de har näst intill alla haft sina egna sätt att beräkna division på. Egyptierna använde till exempel prickar över sina symboler för heltal för att markera att de var bråk, tex kunde iii betyda 1/3.

De beräknade också division på ett speciellt sätt. För att beräkna 27/3 skrev de först upp 1 och 3 i varsin spalt (spalt 1 och spalt 2).

Spalt 1 Spalt 2
1 3
2 6
4 12
8 24

Därefter fördubblades siffrorna i spalterna tills dess att man kunde hitta en summa som är 27 i spalt 2 i vårt fall, dvs 24+3. När detta är gjort så adderade man motsvarande tal i den vänstra spalten och detta ger då kvoten, dvs 1+8=9.

Det man bör nämna är att denna metod endast fungerade så länge talen gick jämnt ut i divisionen, men de använde sig dock av en liknande metod för att räkna ut divisioner med rest.

I Sverige har man använt sig av kort division och lång division för att beräkna olika kvoter. Lång divsion brukar oftast kallas för trappan eller liggande stolen där skillnaden mellan dessa ligger i hur man placerar nämnaren och täljaren i uträkningen.


Division med komplexa tal

Grafisk illustration av ett komplext tal och dess konjugat

Låt oss säga att vi har två komplexa tal z2 och z2 och nu vill beräkna 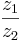\frac{z_1}{z_2}.

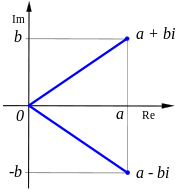
Man märker ganska snabbt att division för komplexa tal inte riktigt fungerar som för de reela talen så det är nu man använder sig utav något som heter komplexkonjugat. Vilket grafiskt kan ses i bilden till höger.

Med hjälp av komplexkonjugatet kan vi skriva kvoten mellan två komplexa tal z1 och z2 med formeln:

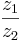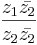\frac{z_1}{z_2} = \frac{z_1\bar{z_2}}{z_2\bar{z_2}} , så länge 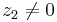z_2\ne0 och där 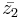\bar{z_2} utgör komplexakonjugatet till z2

Exempel:

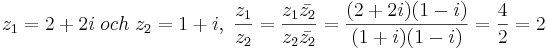
z_1 = 2+2i\;och\;z_2 = 1+i,\; \frac{z_1}{z_2} = \frac{z_1\bar{z_2}}{z_2\bar{z_2}}=\frac{{(2+2i)(1-i)}}{{(1+i)(1-i)}}={4 \over 2}=2


En sak som bör nämnas är att man genom denna metod omvandlar nämnaren till reel och därefter utför reel division på täljarens imaginär och realdel. Ibland som i exemplet ovan försvinner den imaginära delen och man får endast ett reelt svar, men så är inte alltid fallet.

Nämnaren kan heller aldrig bli 0 genom att man förlänger den med dess komplexkonjugat, om inte nämnaren redan var 0. Detta går lättast att förklara genom användandet av konjugatregeln som säger att (a + b)(a − b) = a2 − b2. I detta fall med komplexa tal kommer b utgöra vår imaginär del.

Ett komplext tal i kvadrat ger alltid ett negativt tal, alltså kommer vi då enligt konjugatregeln få a2 − ( − b2), dvs den reela delen minus ett negativt reelt tal. Detta kommer aldrig kunna bli 0, då vi har en addition mellan två positiva tal.


Division med matriser

Precis som tidigare har nämnts så utgör division motsatsen eller inversen till multiplikation. För matriser fungerar inte division riktigt på samma sätt utan där utgör multiplikation med en matrisinvers inversen till matrismultiplikation.

Om A och Y utgör två kända matriser och X är okänd så har matrisekvationen AX = Y lösningen X = A − 1Y, så länge A är inverterbar. Saknar däremot A invers kan matisekvationen sakna lösning eller ha en parameterlösning, om A saknar invers är dess determinant lika med 0 och matrisen A innehåller även rader som är linjärt beroende.


Exempel:

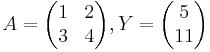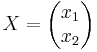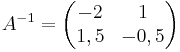Lösningen på AX = Y, där A=\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} , Y=\begin{pmatrix} 5 \\ 11 \end{pmatrix} och X=\begin{pmatrix} x_1 \\ x_2 \end{pmatrix}, fås nu genom att först ta fram inversen A^{-1}=\begin{pmatrix} -2&1 \\ 1,5&-0,5 \end{pmatrix}.

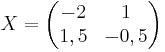
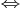
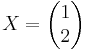
Eftersom X = A − 1Y, så är alltså X=\begin{pmatrix} -2&1 \\ 1,5&-0,5 \end{pmatrix}\begin{pmatrix} 5 \\ 11 \end{pmatrix}\Leftrightarrow X=\begin{pmatrix} 1 \\ 2 \end{pmatrix}

Polynomdivision

Kvoten: 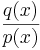\frac{q(x)}{p(x)} kan man få ut genom att använda sig av liggande stolen.

Men denna metod går endast att utnyttja så länge som q(x) har högre eller samma grad som p(x). Om däremot p(x) har högre grad än q(x) får man istället använda metoden partialbråksuppdelning och mer om detta kan läsas i artikeln om polynomdivision.


Derivatan för en kvot mellan funktioner

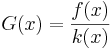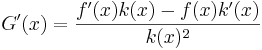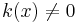
Om vi har en funktion G(x) = \frac{f(x)}{k(x)} så är dess derivata G'(x)= \frac{f'(x)k(x)-f(x)k'(x)}{k(x)^2} ifall k(x)\ne0

Exempel:

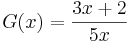G(x) = \frac{3x+2}{5x} har derivatan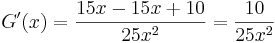 G'(x)= \frac{15x -15x+10}{25x^2}=\frac{10}{25x^2}

Division med bråk

För att beräkna 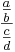{{a \over b}\over {c \over d}} använder man sig av inversen till bråket i nämnaren, så att \frac {\frac a b} {\frac c d} = \frac a b \cdot \frac d c = \frac {ad} {bc}, där a är den enda som kan vara 0.

Exempel:

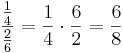\frac {\frac 1 4} {\frac 2 6} = \frac 1 4 \cdot \frac 6 2 = \frac {6} {8},


Notation

  • Med snedstreck a/b\
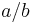
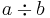
  • Med tecknet ÷ a \div b
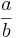
  • Med ett vågrätt (horisontellt) bråkstreck \frac{a}{b}
  • Med kolon a:b\
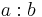
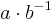
  • Med hjälp av negativa exponenter a\cdot b^{-1}

Övrigt

Operationen kan också utläsas på flera sätt:

  • "a delat/dividerat med/på b"
  • "a genom b"

a kallas täljare eller dividend, b kallas nämnare eller divisor.

Om 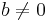b \not = 0 gäller: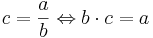 c = \frac{a}{b} \Leftrightarrow b \cdot c = a
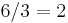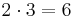Till exempel: 6 / 3 = 2 \ eftersom 2 \cdot 3 = 6.
Detta är oftast det första sättet man lär sig beräkna division på, att tänka "kvoten gånger nämnaren ska bli täljaren".

Vid heltalsdivision kan man skriva

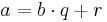a = b \cdot q + r, där a,b,q,r är heltal, och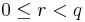 0 \leq r < q

Då kallas q kvoten och r resten (vid division av a med b).

Referenser

  • Forsling, Göran och Neymark, Mats, "Matematisk analys en variabel", 2006, MAI (Linköpings Universitet)
  • Janfalk, Ulf, Linjär Algebra, 2007, MAI (Linköpings Universitet)
  • Motz, Lloyd och Weaver Hane, Jefferson, "The story of Mathematics", 1993
  • Thompson, Jan, " Historiens matematik", 1991
  • http://www.maths.lth.se/query/answers/q200008.html

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Division_(matematik)"
Personliga verktyg