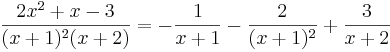Partialbråksuppdelning
Från Rilpedia
Partialbråksuppdelning är en metod som används för att dela upp ett givet bråk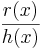 
i så kallade partialbråk. Denna metod är mycket användbar i matematisk analys.
Utgångspunkten är att det givna bråket är ett äkta bråk, det vill säga att täljaren har lägre gradtal än nämnaren och att nämnaren är faktoriserad så långt som möjligt. Målet är att finna partialbråk vars summa motsvarar det ursprungliga bråket.
Partialbråken konstrueras genom att identifiera faktorer i nämnaren enligt följande tabell (alla tal är reella):
| Faktor i nämnaren | Ger upphov till partialbråken |
|---|---|
| x + a |  |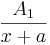
| (x + a)n |  |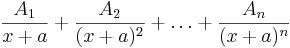
| x2 + ax + b |  |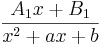
| (x2 + ax + b)n |  |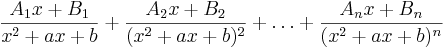
Koefficienterna Ak och Bk är entydigt bestämda (vilket kan bevisas).
Ett konkret exempel
Partialbråksuppdela: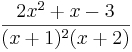 
Vi identifierar faktorer i nämnaren och konstruerar partialbråk (med hjälp av tabellen ovan):
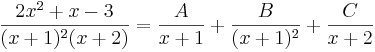
Det som återstår är att bestämma koefficienterna A, B och C. Detta görs enklast genom att multiplicera hela det högra ledet med den ursprungliga nämnaren och sedan ordna alla termer efter dess gradtal. Vi får då:
2x2 + x − 3 = (A + C)x2 + (3A + B + 2C)x + (2A + 2B + C)
Genom att identifiera de termer i både vänster- och högerledet som har samma gradtal bildar vi ett ekvationssystem:
A + C = 2
3A + B + 2C = 1
2A + 2B + C = − 3
Detta system löses lämpligen med successiv elimination, varpå vi får följande ekvivalenta system:
A = − 1, B = − 2, C = 3
Därmed är partialbråksuppdelningen klar:
