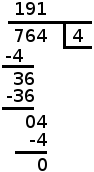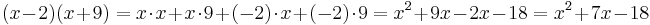Från Rilpedia

Liggande stolen är en matematisk algoritm för att utföra en division. Metoden kan användas för aritmetisk division av godtyckliga tal. Den är även användbar för polynomdivision inom algebran.

Den liggande stolen är ett exempel på så kallad lång uppställning av division, och lämpar sig framförallt för uppgifter där täljaren är flersiffrig. Traditionellt har division med lång uppställning lärts under skolår fyra till sex i den svenska grundskolan. Under senare år har dock skolorna frångått att lära ut lång uppställning, och enligt Skolverket används den idag av endast 1 % av eleverna.^[1] Argumentet för denna förändring är att elever har svårt att förstå lång uppställning samt att kort uppställning ofta fungerar för sådana uppgifter som i praktiken beräknas utan räknehjälpmedel.

I liggande stolen placeras nämnaren till höger om täljaren, och introducerades av dåvarande Skolöverstyrelsen år 1979. Den efterträdde då en tidigare uppställning som gått under namnet "trappan", där nämnaren istället placeras till vänster. Trappan rekommenderades av Skolöverstyrelsen från 1955 till 1979. Matematiskt är trappan och liggande stolen helt likvärdiga, beräkningsstegen är samma, det är bara layouten som skiljer.

Heltalsdivision

Till höger finns ett exempel där 764 skall divideras med 4 med hjälp av liggande stolen. Det går till på följande vis:

1. Vi börjar med att se hur många gånger täljarens första siffra (i det här fallet siffran 7) som nämnaren kan dela. 7 genom 4 blir 1, vilket vi antecknar över 7:an i täljaren.
2. Sedan multiplicerar vi 4 med 1 och subtraherar det från siffran 7, resultatet vi får är 3, som vi flyttar ned till nästa rad och kompletterar med täljarens nästa tal.
3. Vi har nu talet 36 som vi dividerar med 4, vilket går jämnt upp med 9 som vi nu antecknar över täljarens andra siffra (nummer 6).
4. Vi multiplicerar 4 med 9 och subtraherar det från 36, vilket ger talet 0 som vi flyttar ned till raden under.
5. Vi kompletterar det med täljarens sista tal, som är talet 4, och dividerar det med nämnaren som ger kvoten 1.
6. Vi antecknar 1 ovanför täljarens sista siffra (4), multiplicerar 1 med 4 och subtraherar det från ledet.
7. Vi får nu resultatet 0 och har inga tal kvar att använda från täljaren, vår uträkning är klar och divisionens kvot är således 191.

Polynomdivision

Här följer instruktioner för Polynomdivision med hjälp av liggande stolen.

Som exempel använder vi den här formeln: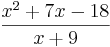

Nu ska vi göra den med liggande stolen.

1. Rita upp stolen.
2. Skriv ut din nämnare och täljare
3. x² delat med x är x och blir det första vi skriver i "kvotfältet"
4. Sedan tar vi hela kvoten vi har multiplicerat med nämnaren och subtraherar det från vår täljare
5. Vi får då en "ny" täljare som vi gör samma sak med.
6. Slutligen får vi 0 i "täljarfältet" och x-2 i "kvotfältet".

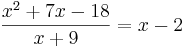
Detta kan kontrolleras genom att multiplicera kvoten med nämnaren och få fram täljaren:

Referenser

1. ↑ Att visa vad man kan. En samling artiklar om ämnesproven i år 5, sidan 107, Skolverket, 2004.