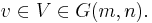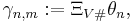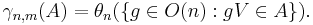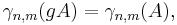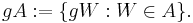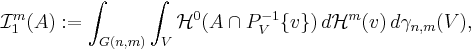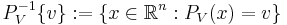Grassmannmått
Från Rilpedia
Version från den 14 april 2009 kl. 14.24 av Novn (Diskussion)
Ett Grassmannmått är ett mått i linjär algebra, namngett efter den tyska matematikern Hermann Grassmann.
Innehåll |
Formell definition
Låt 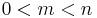 vara heltal och bilda Grassmannmångfalden
vara heltal och bilda Grassmannmångfalden 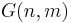 . Definiera en funktion från ortogonalgruppen
. Definiera en funktion från ortogonalgruppen 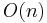 till
till 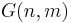 på följande sätt:
på följande sätt:
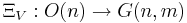 , så att
, så att 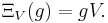
Grassmannmåttet 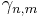 ett bildmått:
ett bildmått:
dvs för 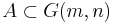
Här är 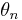 det vridningsinvariant måttet i
det vridningsinvariant måttet i 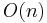 .
.
Egenskaper
- Eftersom måttet
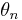 är vridningsinvariant så är Grassmannmåttet också "vridningsinvariant":
är vridningsinvariant så är Grassmannmåttet också "vridningsinvariant":
- för
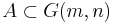 . Här
. Här
- Eftersom Grassmannmåttet är vridningsinvarianta beror det inte på vilket delrum V man väljer. Därför väljer man ofta delrummet
 .
.
Favardmått
Man definierar det Favardmåttet med hjälp av Grassmannmåttet. För heltalen 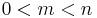 är det m-dimensionella Favardmåttet med en parameter 1 ett Borelmått
är det m-dimensionella Favardmåttet med en parameter 1 ett Borelmått ![\mathcal{I}^m_1 : \mbox{Bor}\,\R^n \rightarrow [0,\infty]](/w/images/sv.rilpedia.org/math/2/e/8/2e8f4d73d031a327612363a4706ab1a2.png) , definierad som:
, definierad som:
där
är måttintegralen med avseende på måttet 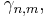
- integralen
är måttintegralen med avseende på det m-dimensionella Hausdorffmåttet  över delrummet
över delrummet 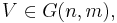
- måttet
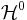 är det nolldimensionella Hausdorffmåttet dvs räknemåttet och
är det nolldimensionella Hausdorffmåttet dvs räknemåttet och
för